Giải SBT Toán lớp 6 Bài 13: Tập hợp các số nguyên
Bài 3.1 trang 48 sách bài tập Toán lớp 6 Tập 1: Diễn đạt lại thông tin sau mà không dùng số âm: “Độ cao trung bình của thềm lục địa Việt Nam là – 65 m”.
Lời giải:
Độ cao trung bình của thềm lục địa Việt Nam là 65 mét dưới mực nước biển.
Bài 3.2 trang 48 sách bài tập Toán lớp 6 Tập 1: Ông Tám nhận được tin nhắn từ ngân hàng về thay đổi số dư trong tài khoản của ông là -210 800 đồng. Em hiểu thế nào về tin nhắn đó?
Lời giải:
Ông Tám nhận được tin nhắn từ ngân hàng về thay đổi số dư trong tài khoản của ông là
-210 800 đồng được hiểu là ông Tám đã rút số tiền 210 800 đồng trong tài khoản.
Bài 3.3 trang 49 sách bài tập Toán lớp 6 Tập 1: Trên hình 3.1, mỗi điểm M, N, P, Q biểu diễn số nguyên nào?
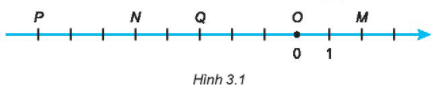
Lời giải:
+) Điểm P nằm bên trái điểm O và cách O một khoảng là 8 đơn vị nên điểm P biểu diễn số – 8
+) Điểm N nằm bên trái điểm O và cách O một khoảng là 5 đơn vị nên điểm N biểu diễn số – 5
+) Điểm Q nằm bên trái điểm O và cách O một khoảng là 3 đơn vị nên điểm Q biểu diễn số – 3
+) Điểm M nằm bên phải điểm O và cách O một khoảng là 2 đơn vị nên điểm P biểu diễn số 2
Bài 3.4 trang 49 sách bài tập Toán lớp 6 Tập 1: Biểu diễn các số sau trên cùng một trục số: 4; -4; -6; 6; -1; 1.
Lời giải:
Các số -6; -4; -1; 1; 4; 6 lần lượt được biểu diễn bởi các điểm A, B, C, D, E, F dưới đây:

Bài 3.5 trang 49 sách bài tập Toán lớp 6 Tập 1: Giả sử một con kiến bò trên một trục số gốc O có chiều dương là chiều từ trái sang phải, chiều ngược lại là chiều âm và giả sử nó đi được 16 đơn vị thì dừng lại. Hỏi trong mỗi trường hợp sau, con kiến dừng lại ở điểm nào trên trục số?
a) Con kiến xuất phát từ gốc O và đi theo chiều dương;
b) Con kiến xuất phát từ gốc O và đi theo chiều âm.
Lời giải:
a) Con kiến xuất phát từ gốc O và đi theo chiều dương, nó đi được 16 đơn vị thì con kiến dừng lại ở điểm 16 trên trục số.
b) Con kiến xuất phát từ gốc O và đi theo chiều âm, nó đi được 16 đơn vị thì con kiến dừng lại ở điểm -16 trên trục số.
Bài 3.6 trang 49 sách bài tập Toán lớp 6 Tập 1: Liệt kê các phần tử của tập hợp sau theo thứ tự tăng dần:
M = {x ∈ Z| x có tận cùng là 2 và -15 < x ≤ 32}
Lời giải:
Các số nguyên có chữ số tận cùng là 2 thỏa mãn -15 < x ≤ 32 là: – 12; – 2; 2; 12; 22; 32
Do đó x {- 12; – 2; 2; 12; 22; 32}
Mà x ∈ M nên M = {- 12; – 2; 2; 12; 22; 32}
Vậy M = {- 12; – 2; 2; 12; 22; 32}.
Bài 3.7 trang 49 sách bài tập Toán lớp 6 Tập 1: So sánh hai số: – 46 789 và – 45 999.
Lời giải:
So sánh các cặp số cùng hàng theo thứ tự từ trái sang phải, ta thấy ở hàng chục nghìn giống nhau cùng là chữ số 4, ở hàng nghìn ta thấy 6 > 5 nên 46 789 > 45 999.
Do đó – 46 789 < – 45 999.
Lý thuyết Tập hợp các số nguyên
1. Làm quen với số nguyên âm
– Các số tự nhiên (khác 0) 1; 2; 3; 4; … còn được gọi là các số nguyên dương.
– Các số – 1; -2; -3; … gọi là các số nguyên âm.
– Tập hợp gồm các số nguyên âm, số 0 và số nguyên dương gọi là tập hợp số nguyên.
Z = {…; -3; -3; -3; 0; 1; 2; 3;…}.
Chú ý:
Số 0 không là số nguyên âm, cũng không phải là số nguyên dương.
Đôi khi ta còn viết thêm dấu “+” ngay trước một số nguyên dương. Chẳng hạn số 6 còn được viết là +6 (đọc là “dương sáu”).
Ví dụ 1. Các số nguyên nào biểu diễn các đại lượng sau:
a) Đỉnh núi Phan – xi – păng cao 3 147, 3m;
b) Độ sâu của đáy sông Sài Gòn là 20m;
c) Bác An đang nợ 2 triệu đồng.
Lời giải
a) Độ cao củ đỉnh núi Phan – xi – păng được biểu diễn là: 3 147, 3m.
b) Độ sâu của đáy sông Sài Gòn được biểu diễn là: -20 m.
c) Số tiền nợ của bác An được biểu diễn là: – 2 (triệu đồng).
2. Thứ tự trong tập số nguyên
Trục số:
Ta biểu diễn các số 0; 1; 2; 3; 4; 5 … và các số nguyên âm -1; -2; -3; 4; 5… như sau:
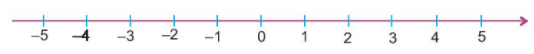
+ Chiều từ trái sang phải là chiều dương, chiều ngược lại là chiều âm.
+ Điểm biểu diễn số nguyên a được gọi là điểm a.
+ Cho hai số nguyên a và b. Trên trục số, nếu điểm a nằm trước điểm b thì số a nhỏ hơn số b, kí hiệu a < b.
Ví dụ 2. Các điểm A, B, C, D và E trong hình biểu diễn những số nào?

Lời giải
Điểm A cách điểm 0 năm đơn vị về bên phải nên A biểu diễn cho số 5;
Điểm C cách điểm 0 bảy đơn vị về bên phải nên C biểu diễn cho số 7;
Điểm B cách điểm 0 bốn đơn vị về bên trái nên B biểu diễn cho số -4;
Điểm E biểu diễn cho điểm – 1;
Điểm D biểu diễn cho điểm 0;
So sánh hai nguyên:
Mọi số nguyên âm đều nhỏ hơn 0, do đó nhỏ hơn mọi số nguyên dương.
Nếu a, b là hai số nguyên dương và a > b thì – a < – b.
Ví dụ 2. Sắp xếp các số sau theo thứ tự tăng dần:
– 3; 4; -9; 0; -12; 2; 15; 1.
Lời giải
Các số đã cho được sắp xếp theo thứ tự tăng dần là:
-12; -9; -3; 0; 1; 2; 4; 15.