1. Giải bài 2.6 trang 104 SBT Giải tích 12
Tìm tập xác định của các hàm số sau:
a) \(y=(x^2-4x+3)^{-2}\)
b) \(y=(x^3-8)^{\frac{\pi} 3}\)
c) \(y=(x^3-3x^2+2x)^{\frac 1 4}\)
d) \(y=(x^2+x-6)^{-\frac 1 3}\)
Phương pháp giải
Sử dụng lý thuyết về tập xác định của hàm số lũy thừa.
+ Lũy thừa có số mũ nguyên dương thì cơ số tùy ý.
+ Lũy thừa có số mũ nguyên âm hoặc bằng 0 thì cơ số khác 0.
+ Lũy thừa có số mũ không nguyên thì cơ số phải dương.
Hướng dẫn giải
a) ĐKXĐ:
\(x^2-4x+3\ne 0\Leftrightarrow x\notin \{1;3\}\)
TXĐ: \(\mathbb{R}\backslash \left\{ 1;3 \right\}\)
b) ĐKXĐ: \(x^3-8>0\Rightarrow x^3>8\Leftrightarrow x > 2\)
TXĐ: \((2;+\infty)\)
c) ĐKXĐ: \(x^3-2x^2+2x>0\Rightarrow x(x^2-2x+2)>0\Rightarrow x > 0\)
(vì \(x^2-2x+2=(x-1)^2+1>0\,\,\forall x\in \mathbb R\))
TXĐ: \((0;+\infty)\)
d) ĐKXĐ: \(x^2+x-6>0\Rightarrow x\in (-\infty;-3)\cup (2;+\infty)\)
TXĐ: \((-\infty;-3)\cup (2;+\infty)\)
2. Giải bài 2.7 trang 104 SBT Giải tích 12
Tính đạo hàm của các hàm số cho ở bài tập 2.6
a) \(y=(x^2-4x+3)^{-2}\)
b) \(y=(x^3-8)^{\frac{\pi} 3}\)
c) \(y=(x^3-3x^2+2x)^{\frac 1 4}\)
d) \(y=(x^2+x-6)^{-\frac 1 3}\)
Phương pháp giải
Áp dụng: \((u^\alpha)’=\alpha.u’.u^{\alpha -1}\)
Hướng dẫn giải
a)
\(y’=-2(2x-4)(x^2-4x+3)^{-2-1}=-2(2x-4)(x^2-4x+3)^{-3}\)
b)
\(y’=\dfrac{\pi} 3 .3x^2.(x^3-8)^{\frac\pi 3-1}=\pi x^2(x^3-8)^{\frac{\pi-3}3}\)
c)
\(y’=\dfrac 1 4 (3x^2-6x+2).(x^3-3x^2+2x)^{\frac 1 4 -1}\\ =\dfrac 1 4(3x^2-6x+2).(x^3-3x^2+2x)^{-\frac 3 4}\)
d)
\(y’=-\dfrac 1 3(2x+1)(x^2+x-6)^{-\frac 1 3 -1}\\ =-\dfrac 1 3 (2x+1)(x^2+x-6)^{-\frac 4 3}\)
3. Giải bài 2.8 trang 104 SBT Giải tích 12
Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau :
a) \(y=x^{-3}\)
b) \(y=x^{-\frac 1 2}\)
c) \(y=x^{\frac {\pi} 4}\)
Phương pháp giải
Các bước khảo sát sự biến thiên và vẽ đồ thị hàm số:
– Tìm tập xác định
– Tính đạo hàm
– Tìm giới hạn xác định các tiệm cận (nếu có)
– Lập bảng biến thiên
– Vẽ đồ thị
Hướng dẫn giải
a)
\(y=x^{-3}=\dfrac1 {x^3}\)
TXĐ: \(D=\mathbb{R}\backslash \left\{ 0 \right\}\)
Hàm số đã cho là hàm lẻ vì \(y(x)=-y(-x)\)
\(y’=-3x^{-4}=-\dfrac 3 {x^4}<0\,\,\forall x\in D\)
\(\lim\limits_{x\to 0^-}y=-\infty; \lim\limits_{x\to 0^+}y=+\infty\\ \lim\limits_{x\to -\infty}y=\lim\limits_{x\to +\infty}y=0\)
Đồ thị có tiệm cận đứng là trục tung và tiệm cận ngang là trục hoành.
Bảng biến thiên
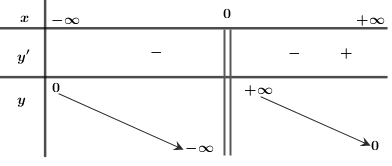
Đồ thị nhận gốc O là tâm đối xứng
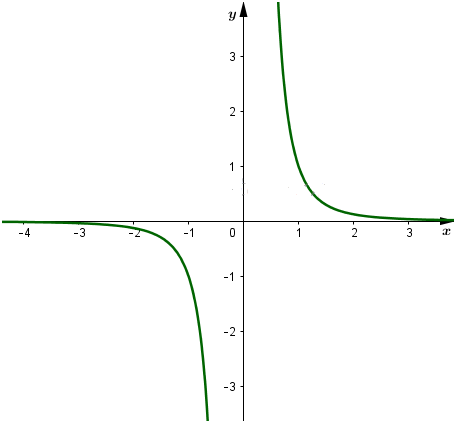
b)
\(y=x^{-\frac 1 2}=\dfrac1 {\sqrt x}\)
TXĐ: \(D=(0;+\infty)\)
\(y’=-\dfrac 1 2x^{-\frac 3 2}=-\dfrac 1 {2\sqrt{x^3}}<0\,\,\forall x\in D\)
\(\lim\limits_{x\to 0}y=+\infty\\ \lim\limits_{x\to +\infty}y=0\)
Đồ thị có tiệm cận đứng là trục tung và tiệm cận ngang là trục hoành.
Bảng biến thiên
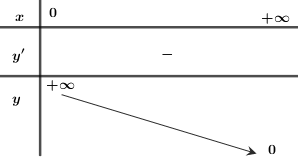
Đồ thị
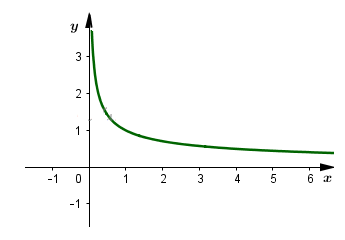
c)
\(y=x^{\frac \pi 4}\)
TXĐ: \(D=(0;+\infty)\)
\(y’=\dfrac {\pi} 4 x^{\frac \pi 4 -1} > 0\,\,\forall x\in D\)
\(\lim\limits_{x\to 0}y=0\\ \lim\limits_{x\to+\infty}y=+\infty\)
Đồ thị không có tiệm cận
Bảng biến thiên

Đồ thị
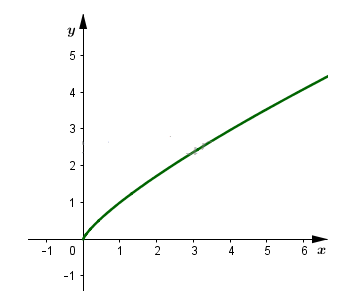
4. Giải bài 2.9 trang 104 SBT Giải tích 12
Vẽ đồ thị của các hàm số \(y=x^2\) và \(y=x^{\frac 1 2}\) trên cùng một hệ trục tọa độ. Hãy so sánh giá trị của các hàm số đó khi \(x=0,5;1;\dfrac 3 2; 2; 3; 4\)
Phương pháp giải
– Vẽ đồ thị các hàm số đã cho dựa vào kiến thức đã học về hàm số bậc hai và hàm số lũy thừa.
– So sánh giá trị của hai hàm số tại các điểm \(x = {x_i}\) bằng cách dựng đường thẳng \(x = {x_i}\) và nhận xét vị trí các điểm giao trên hình vẽ.
Hướng dẫn giải
+) Vẽ đồ thị hàm số \(y=x^{2}\)
TXĐ: \(D=\mathbb R\)
Hàm số là hàm chẵn vì \(y(x)=y(-x)\)
\(y’=2x\\ y’=0\Rightarrow x=0\)
\(\lim\limits_{x\to -\infty}y= \lim\limits_{x\to +\infty}y=+\infty\)
Đồ thị không có tiệm cận, nhận trục tung là trục đối xứng.
Bảng biến thiên
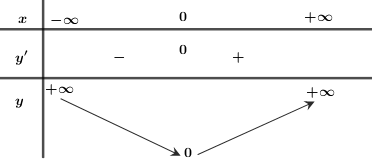
+) Vẽ đồ thị hàm số \(y=x^{\frac 12}\)
TXĐ: \(D=(0;+\infty)\)
\(y’=\dfrac 1 2 x^{-\frac 1 2}=\dfrac {1}{2\sqrt x}\)
\(\lim\limits_{x\to 0}y=0 \\ \lim\limits_{x\to +\infty}y=+\infty\)
Đồ thị không có tiệm cận
Bảng biến thiên
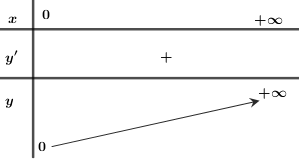
Đồ thị hai hàm số:
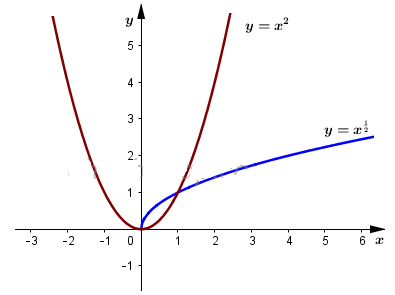
Đặt \(f(x)=x^2; g(x)=x^{\frac 1 2}\)
\(\bullet\)Tại \(x=0,5\):
\(f(0,5)=0,5^2; g(0,5)=0,5^{\frac 1 2}\)
Vì \(0<0,5<1\) và \(2>\dfrac 1 2\) nên \(f(0,5)< g(0,5)\)
\(\bullet\)Tại \(x=1\):
\(f(1)=1^2=1; g(1)=1^{\frac 1 2}=1\)
Nên \(f(1)= g(1)\)
\(\bullet\)Tại \(x=\dfrac 3 2\):
\(f\left(\dfrac 3 2\right)=\left(\dfrac 3 2\right)^2; g\left(\dfrac 3 2\right)=\left(\dfrac 3 2\right)^{\frac 1 2}\)
Vì \(\dfrac 3 2>1\) và \(2>\dfrac 1 2\) nên \(f\left(\dfrac 3 2\right)> g\left(\dfrac 3 2\right)\)
Từ đồ thị hàm số nhận thấy từ giá trị \( x= 1\) trở đi, hàm số \(y=f(x)\) luôn lớn hơn \(y=g(x\)). Hay
\(f(2)>g(2)\\ f(3)>g(3)\\ f(4)>g(4)\)
5. Giải bài 2.10 trang 104 SBT Giải tích 12
Tìm x, sao cho \(x^{-4}=16\).
A. \(x=2\)
B. \(x=-2\)
C. \(x=\dfrac 1 2\)
D. \(x=4\)
Phương pháp giải
Biến đổi phương trình về dạng \({x^n} = {a^n} \Leftrightarrow x = \pm a\) với n chẵn.
Hướng dẫn giải
Ta có:
\(x^{-4}=16\\ \Rightarrow \dfrac 1 {x^4}=\dfrac 1{16}\\ \Leftrightarrow x=\dfrac 1 2\)
Chọn C.
6. Giải bài 2.11 trang 104 SBT Giải tích 12
Tìm số lớn nhất trong các số: \(0,3^{\pi};0,3^{0,5}; 0,3^{\frac 2 3}; 0,3 ^{3,1415}\)
A. \( 0,3^{\pi}\)
B. \(0,3^{0,5}\)
C. \(0,3^{\frac 2 3}\)
D. \(0,3 ^{3,1415}\)
Phương pháp giải
Sử dụng tính chất so sánh lũy thừa: Nếu 0 < a < 1 thì \({a^m} > {a^n} \Leftrightarrow m < n\)
Hướng dẫn giải
Vì \(0<0,3<1\) và \(0,5<\dfrac 2 3 < 3,1415<\pi\)
Nên giá trị lớn nhất trong các số là \(0,3^{0,5}\)
Chọn B
7. Giải bài 2.12 trang 104 SBT Giải tích 12
Tìm số nhỏ nhất trong các số: \(\sqrt{2^\pi}\); \(1,9^\pi\); \(\left(\dfrac 1 {\sqrt 2}\right)^\pi\); \(\pi ^\pi\)
A. \(\sqrt{2^\pi}\)
B. \(1,9^\pi\)
C. \(\left(\dfrac 1 {\sqrt 2}\right)^\pi\)
D. \(\pi ^\pi\)
Phương pháp giải
Sử dụng so sánh lũy thừa: Nếu n > 0 thì \({a^n} < {b^n} \Leftrightarrow a < b\)
Hướng dẫn giải
Ta có: \(\dfrac 1{\sqrt 2}<\sqrt 2<1,9<\pi\)
Số nhỏ nhất trong các số là \(\sqrt{2^\pi}\)
Chọn A.
8. Giải bài 2.13 trang 104 SBT Giải tích 12
Tìm khẳng định đúng trong các khẳng định sau :
A. \(5^{-2}>5^{-0,7}\)
B. \(5^{\frac 1 3}<\left(\dfrac 1 5 \right)^{2,1}\)
C. \(2^\pi > e^\pi\)
D. \(\pi ^{\frac 1 2}>1\)
Phương pháp giải
Nhận xét tính đúng sai của từng đáp án, sử dụng tính chất so sánh lũy thừa:
+) Nếu a > 1 thì \({a^m} > {a^n} \Leftrightarrow m > n\)
+) Nếu \(n > 0,n \notin \mathbb{Z}\) thì \({a^n} > {b^n} \Leftrightarrow a > b > 0\)
Hướng dẫn giải
\(\left\{\begin{align} &5> 1\\& -2<-0,7\\ \end{align}\right.\Rightarrow 5^{-2}<5^{-0,7}\)
A – sai
\(\left(\dfrac 1 5\right)^{2,1}=5^{-2,1}\\ \left\{\begin{align} &5> 1\\&\dfrac 1 3 > -2,1\\ \end{align}\right.\Rightarrow 5^{\frac 1 3}>5^{-2,1}\)
B – sai
\(e\approx 2,71>2\Rightarrow 2^\pi < e^\pi\)
C – sai
\(\pi^{\frac 1 2}>1^{\frac 1 2}=1\)
D – đúng
Chọn D.
9. Giải bài 2.14 trang 104 SBT Giải tích 12
Tìm khẳng định sai trong các khẳng định sau :
A. \(0,5 ^{-\frac 2 3}> 0,6^{-\frac 2 3}\)
B. \(36^{-\frac 4 5}< \pi^{-\frac 4 5}\)
C. \(e^{\frac 1 2}<2\)
D. \((\sqrt 2 ) ^{-\frac 3 4}<1\)
Phương pháp giải
Nhận xét tính đúng sai của từng đáp án, sử dụng tính chất so sánh lũy thừa:
+) Nếu a > 1 thì \({a^m} > {a^n} \Leftrightarrow m > n\)
+) Nếu \(n > 0,n \notin \mathbb{Z}\) thì \({a^n} > {b^n} \Leftrightarrow a > b > 0\)
Hướng dẫn giải
\(0<0,5<0,6<1\) nên \(0,5 ^{-\frac 2 3}>0,6^{-\frac 2 3}\)
A – đúng
\(36> \pi>1\Rightarrow 36^{-\frac 4 5}> \pi^{-\frac 4 5}\)
B – sai
\(e< 4\Rightarrow e^{\frac 1 2 }< 4^{\frac 1 2}=2\)
C – đúng
\(\sqrt 2 > 1 \Rightarrow (\sqrt 2)^{-\frac 3 4}<1\)
D – đúng
Chọn B
