CÁC BẠN HỌC SINH LUYỆN TẬP, MỖI LẦN LÀM BÀI ĐỀU THAY ĐỔI CÂU, ĐÁP ÁN. ĐỀ CÓ 22 CÂU NHƯ THI TNTHPT 2025.
==============
Phần I. Trắc nghiệm đơn chọn
Cho \(a\) là số thực dương. Mệnh đề nào dưới đây sai?
Với \(a > 0\), biểu thức \(\cann{3}{a^{\frac{1}{2}} \cdot \sqrt a } \cdot {a^{\frac{4}{3}}}\) viết dưới dạng một luỹ thừa là
Cho \(a,b\) là các số thực dương, trong đó \(a \ne 1\). Mệnh đề nào dưới đây sai?
Cho \({\rm{lo}}{{\rm{g}}_a}b = 3\) và \({\rm{lo}}{{\rm{g}}_a}c = 4\). Tính \(P = {\rm{lo}}{{\rm{g}}_a}\left( {{b^3}{c^2}} \right)\).
Nghiệm của phương trình \({2^{4x + 5}} = \frac{1}{8}\) là
Nghiệm của phương trình \({\rm{lo}}{{\rm{g}}_2}{x^3} - 2{\rm{lo}}{{\rm{g}}_2}x = 3\) là
Tập nghiệm \(S\) của bất phương trình \({\left( {\frac{1}{3}} \right)^{3x - 1}} < {\left( {\frac{1}{3}} \right)^{2x}}\) là
Tập nghiệm của bất phương trình \({\rm{log}}\left( {4x + 1} \right) \ge {\rm{log}}\left( {3x + 5} \right)\) là
Hàm số nào sau đây nghịch biến trên khoảng \(\left( {0; + \infty } \right)\)?
10
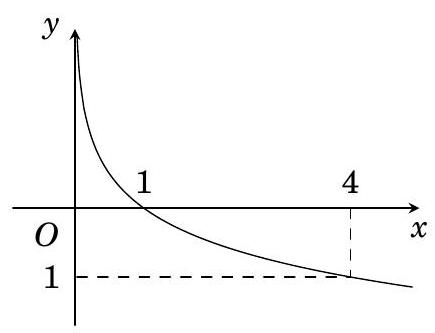
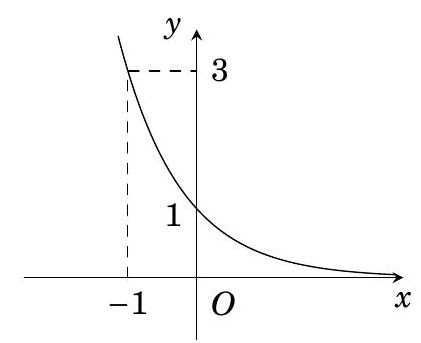
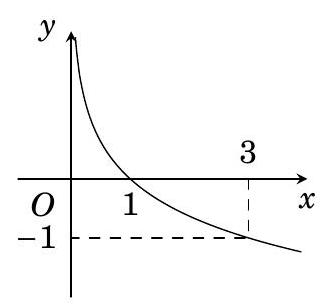
Hàm số nào sau đây có đồ thị như hình vẽ bên? 
Tập xác định của hàm số \(y = {\rm{lo}}{{\rm{g}}_7}\left( {2x - 1} \right)\) là
Độ pH của một dung dịch được tính theo công thức: \({\rm{pH}} = - {\rm{log}}[ {{H^ + }} ]\)trong đó \([ {{H^ + }} ]\)là nồng độ ion hydrogen. Người ta đo được độ pH của nước ép cà chua là 4, bột nở (baking Soda) là 8. Nồng độ ion hydrogen của nước ép cà chua gấp bao nhiêu lần bột nơ?
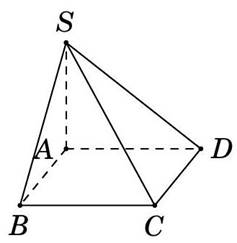
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\sqrt 3 \),\(SA = a\) và \(SA \bot \left( {ABCD} \right)\). Góc giữa hai đường thẳng \(CD\) và \(SB\) bằng 
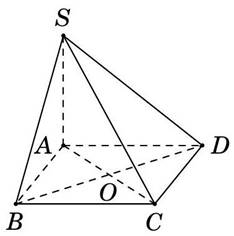
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\), cạnh bên \(SA\) vuông góc với mặt phẳng đáy. Khoảng cách từ \(B\) đến mặt phẳng (SAC) bằng 
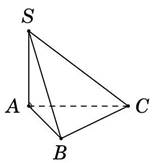
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), \(SA \bot \left( {ABC} \right)\) và \(SA = \frac{{a\sqrt 3 }}{2}\). Góc phẳng nhị diện \([ {A,BC,S} ]\) bằng 
25
Cho \(a\) là số thực dương. Mệnh đề nào dưới đây sai?
Với \(a > 0\), biểu thức \(\cann{3}{a^{\frac{1}{2}}} \cdot {a^{\frac{4}{3}}}\) viết dưới dạng một luỹ thừa là
Cho \(a,b\) là các số thực dương, trong đó \(a \ne 1\). Mệnh đề nào dưới đây sai?
Cho \({\rm{lo}}{{\rm{g}}_a}b = 2\) và \({\rm{lo}}{{\rm{g}}_a}c = 4\). Tính \(S = {\rm{lo}}{{\rm{g}}_a}\left( {b \cdot {c^4}} \right)\).
Nghiệm của phương trình \({5^{x + 5}} = 25\) là
Nghiệm của phương trình: \(2{\rm{lo}}{{\rm{g}}_4}x = 3\) là
Tập nghiệm \(S\) của bất phương trình \({\left( {\frac{1}{7}} \right)^{2x - 1}} \ge 1\) là
Tập nghiệm của bất phương trình \({\rm{lo}}{{\rm{g}}_2}\left( {2x + 1} \right) \ge {\rm{lo}}{{\rm{g}}_2}\left( {x + 4} \right)\) là
Hàm số nào sau đây đồng biến trên khoảng \(\left( {0; + \infty } \right)\)?
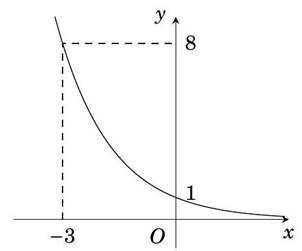
Hàm số nào sau đây có đồ thị như hình vẽ bên? 
Tập xác định của hàm số \(y = {\rm{lo}}{{\rm{g}}_{\frac{1}{2}}}\left( {x - 7} \right)\) là
Độ pH của một dung dịch được tính theo công thức: \({\rm{pH}} = - {\rm{log}}[ {{H^ + }} ]\)trong đó \([ {{H^ + }} ]\)là nồng độ ion hydrogen. Người ta đo được độ pH của nước Cất là 7, nước Coca là 5,8. Nồng độ ion hydrogen của nước Cất gấp bao nhiêu lần Coca?
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(SA \bot \left( {ABCD} \right)\). Mệnh đề nào dưới đây sai? 
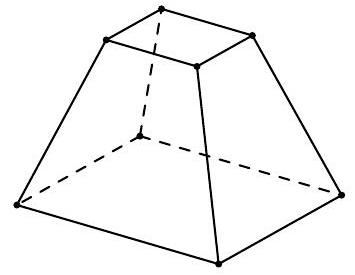
Một cái hầm có dạng hình chóp cụt tứ giác đều với cạnh đáy lớn bằng \(10\left( {{\rm{m}}} \right)\), cạnh đáy nhỏ bằng \(5\left( {{\rm{m}}} \right)\) và chiều cao bằng \(3\left( {{\rm{m}}} \right)\). Thể tích cái hầm bằng 
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\), cạnh bên \(SA\) vuông góc với mặt phẳng đáy. Khoảng cách từ \(B\) đến mặt phẳng (SAC) bằng 
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), \(SA \bot \left( {ABC} \right)\) và \(SA = \frac{{3a}}{2}\). Góc phẳng nhị diện [A,BC,S] bằng 
Phần II.
Cho hàm số \(f\left( x \right) = {a^x}\) có đồ thị như hình vẽ bên 
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật tâm \(O\), \(SA \bot \left( {ABCD} \right)\) và \(SA = AB = a,AD = 6a\). 
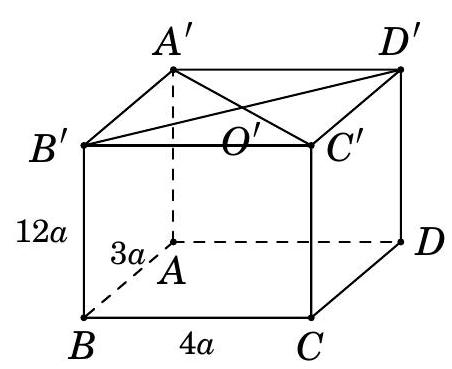
Cho hình hộp chữ nhật \(ABCD \cdot A'B'C'D'\) có ba kích thước \(AB = 3a,BC = 4a,BB' = 12a\). Gọi \(O'\) là tâm hình chữ nhật \(A'B'C'D'\). 
Cho hàm số \(f\left( x \right) = {\rm{lo}}{{\rm{g}}_a}x\) có đồ thị như hình vẽ bên 
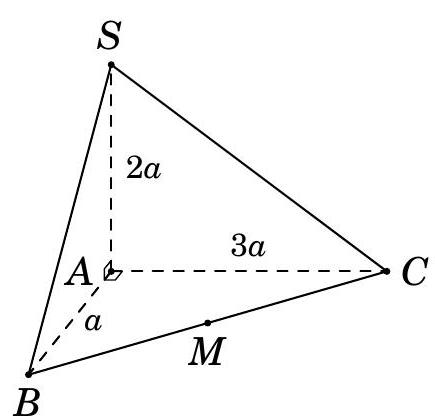
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là là tam giác vuông tại \(A\). Gọi \(M\) là trung điểm \(BC\). Biết \(SA \bot \left( {ABC} \right)\) và \(SA = 2a,AB = a,AC = 3a\) (tham khảo hình vẽ). 
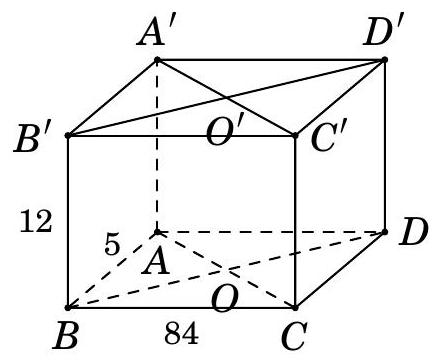
Cho hình hộp chữ nhật \(ABCD \cdot A'B'C'D'\) có ba kích thước \(AB = 5\left( {{\rm{cm}}} \right),BC = 84\left( {{\rm{cm}}} \right),BB' = 12\left( {{\rm{cm}}} \right)\). Gọi \(O,O'\) là tâm hình chữ nhật \(ABCD\) và \(A'B'C'D'\) (tham khảo hình bên). 
PHẦN III