Đề Thi thử Môn Toán TN THPT – 2025

By

Đề Thi thử Môn Toán TN THPT – 2025


PHẦN I. Thí sinh trả lời từ câu 1 đến Câu 12. Mỗi câu chỉ chọn một phương án.

Trong không gian với hệ trục tọa độ \(Oxyz\), khoảng cách từ điểm \(M(1; 2; 4)\) đến mặt phẳng \((P): ax + by + cz + d = 0\) \((a, b, c, d \in \mathbb{R})\) bằng
Họ nguyên hàm của hàm số \(f(x) = 5^x\) bằng
Cho cấp số nhân \((u_n)\) có \(u_1 = 1\) và \(u_2 = 3\). Số hạng \(u_4\) của cấp số nhân là
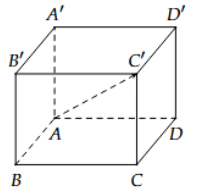
Cho hình hộp \(ABCD. A'B'C'D'\) như hình bên:
Vectơ \(\vec{u} = \overrightarrow{AC'} - (\overrightarrow{AB} + \overrightarrow{AA'})\) cùng hướng với vectơ nào sau đây?
Cho một mẫu số liệu ghép nhóm có phương sai là \(2{,}25\). Độ lệch chuẩn của mẫu số liệu đó bằng
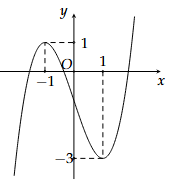
Cho hàm số bậc ba \(y = f(x)\) có đồ thị như hình bên.
Điểm cực đại của hàm số đã cho là
Nghiệm của phương trình \(\tan x = -\sqrt{3}\) là
Tập nghiệm \(S\) của bất phương trình \(\log_{\frac{1}{2}}(x - 3) \leq \log_{\frac{1}{2}}5\) là
Đồ thị của hàm số \( y = \dfrac{2x - 1}{x - 1} \) có tiệm cận đứng là đường thẳng nào?
Trong không gian \( Oxyz \), vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng có phương trình \( \dfrac{x - 2}{3} = \dfrac{y + 3}{-4} = \dfrac{z - 4}{5} \)?
Nếu hàm số \( y = f(x) \) liên tục và nhận giá trị dương trên tập số thực thì diện tích hình phẳng giới hạn bởi đồ thị hàm số, trục hoành và các đường thẳng \( x = 1 \), \( x = 4 \) bằng
Cho hình chóp \( S.ABCD \) có \( SA \perp (ABCD) \). Khi đó, \( SA \) vuông góc với đường thẳng nào sau đây?


PHẦN II. Thí sinh trả lời từ câu 13 đến câu 16. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Trong không gian với hệ trục tọa độ \( Oxyz \) (đơn vị trên mỗi trục tính bằng mét), một trạm phát sóng wifi được đặt ở vị trí \( I \), phương trình mặt cầu mô tả ranh giới vùng phủ sóng là \( (S): (x+10)^2 + (y - 5)^2 + z^2 = 2500 \). Anh Sơn di chuyển thẳng từ vị trí \( A(125; 70; 0) \) đến vị trí \( B(25; -10; 0) \) với vận tốc không đổi là \(1{,}2 \)m/s.
Một xe ô tô đang chạy với vận tốc \(54 \, \text{km/h}\) thì người lái xe đạp phanh. Kể từ thời điểm này, ô tô chuyển động chậm dần đều với gia tốc \( a(t) = -5 \, \text{m/s}^2 \). Gọi \( v(t) \) là vận tốc của xe từ lúc đạp phanh đến lúc dừng hẳn (trong đó \( t \) là thời gian tính bằng giây kể từ lúc đạp phanh).
Một trường đại học đã tổ chức một cuộc khảo sát về mức độ hài lòng của sinh viên đối với dịch vụ thư viện. Kết quả cho thấy \(40\)% sinh viên hài lòng với dịch vụ. Trong cuộc khảo sát này, \(60\)% sinh viên là nữ, trong đó \(50\)% hài lòng với dịch vụ. Người ta chọn ngẫu nhiên một sinh viên tham gia khảo sát và xét các biến cố: \(A\): Sinh viên được chọn là nữ; \(B\): Sinh viên được chọn hài lòng với dịch vụ.
Cho hàm số \( f(x) = \mathrm{e}^x - 3x + 1 \).


Phần III: Trả lời ngắn


Một công ty vận tải cần giao hàng đến tất cả các địa điểm \(A\), \(B\), \(C\), \(D\), \(E\) (tham khảo hình vẽ).
Chi phí di chuyển giữa các địa điểm này được mô tả trên hình (tính theo đơn vị nghìn đồng). Xe giao hàng của công ty xuất phát từ \(E\), đi qua tất cả các địa điểm còn lại đúng một lần sau đó trở lại \(E\). Tìm chi phí thấp nhất của xe giao hàng (tính theo đơn vị nghìn đồng).

Cho hình chóp \(S.ABC\) có \(AB = 6\), \(BC = 8\), \(CA = 10\). Tam giác \(SAB\) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng \(SC\) và mặt phẳng \((ABC)\) bằng bao nhiêu độ (làm tròn đến hàng đơn vị)?
Một công ty đã đặt hàng việc xây dựng logo doanh nghiệp của mình bằng gỗ và đồng thiết kế theo mẫu bên dưới.
Hình tròn sẽ làm bằng gỗ có tâm tại điểm \(O(0;0)\). Phần làm bằng đồng (là phần tô đậm) được giới hạn bởi đồ thị hàm số \(y = x^3 - x\) và đường thẳng có phương trình \(y = x\). Biết rằng 1 mét vuông tấm đồng có giá \(600\,000\) đồng và không bị hao phí; chi phí nhân công làm phần đồng là \(30\)% so với giá tiền tấm đồng, và chi phí cho hình tròn bằng gỗ, vận chuyển và lắp đặt tại chỗ là một khoản cố định là \(2\,700\,000\) đồng.
Hỏi công ty phải trả bao nhiêu triệu đồng cho việc chế tạo và lắp đặt logo doanh nghiệp của mình?
Giả sử giá của một cổ phiếu nào đó (tính bằng euro) trong một ngày nhất định (có 8 giờ giao dịch) được mô tả bởi hàm số: \(f(x) = 35{,}7 \dfrac{x+2}{x^2+21}\), \(x \in [ 0;8 ]\), trong đó \(x\) là thời gian (tính bằng giờ) kể từ khi phiên giao dịch mở cửa. Nếu một người mua \(100\) cổ phiếu và bán chúng ngay trong ngày này thì người đó có lợi nhuận tối đa là bao nhiêu euro?
Trong không gian \(Oxyz\), cho tứ diện \(ABCD\) có \(A(3;3;9)\), \(B(-1;1;6)\), \(C(2;1;0)\), và \(D(-3;6;0)\). Tính khoảng cách từ điểm \(A\) đến mặt phẳng \((BCD)\).

Trong một trường THPT A, tỷ lệ học sinh nữ là \(45\)%. Tỷ lệ học sinh nữ và tỷ lệ học sinh nam tham gia câu lạc bộ Tiếng Anh lần lượt là \(10\)% và \(8\)%. Gặp ngẫu nhiên một học sinh của trường, biết rằng học sinh đó có tham gia câu lạc bộ Tiếng Anh, tính xác suất học sinh đó là nam (làm tròn kết quả đến hàng phần trăm).


Menu
Tài khoản