Đề Luyện tập thi HK2 – Toán 11 – online
Đề Luyện tập thi HK2 – Toán 11 – online
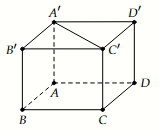
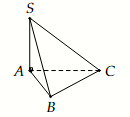 Vậy thể tích khối chóp $V=\dfrac{1}{6}SA\cdot BC \cdot AB=\dfrac{1}{6}\cdot 12\cdot 12 \cdot 9=216(\mathrm{m}^3)$.
Vậy thể tích khối chóp $V=\dfrac{1}{6}SA\cdot BC \cdot AB=\dfrac{1}{6}\cdot 12\cdot 12 \cdot 9=216(\mathrm{m}^3)$.Điểm nhóm trắc nghiệm đơn chọn: 0
Điểm nhóm đúng/sai: 0
Điểm nhóm trả lời ngắn: 0
Tổng điểm bài thi: 0