Xác định Parabol (P): y=ax2+bx+2 biết rằng Parabol đi qua hai điểm M(1;5) và N(2;−2).

Câu hỏi:

Xác định Parabol (P): $y=a{x}^2+bx+2$biết rằng Parabol đi qua hai điểm M(1;5) và N(2;−2).

A. $y=-5x^2+8x+2$

Đáp án chính xác

B. $y=10x^2+13x+2$

C. $y=-10x^2-13x+2$

D. $y=9x^2+6x-5$

Trả lời:

Vì nên tọa độ của hai điểm M, N phải thỏa mãn phương trình của (P).
Do đó, ta có hệ phương trình $\left\{\begin{array}{c}5=a+b+2\\ -2=4a+2b+2\end{array}\right.\iff \left\{\begin{array}{c}a=-5\\ b=8\end{array}\right.$

Vậy phương trình của (P) là:  $y=-5x^2+8x+2$

Đáp án cần chọn là: A

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Xác định Parabol (P): y=ax2+bx+3  biết rằng Parabol có đỉnh I(3;−2).
   
   

   Câu hỏi:
   

   Xác định Parabol (P): $y=a{x}^2+bx+3$ biết rằng Parabol có đỉnh I(3;−2).

   A. $y=x^2-6x+3$

   B. $y=-\frac{5}{9}{x}^2+\frac{10}{3}x+3$

   C. $y=3x^2+9x+3$

   D. $y=\frac{5}{9}{x}^2-\frac{10}{3}x+3$

   Đáp án chính xác

   Trả lời:

   Ta có đỉnh của (P)có tọa độ
   $\left\{\begin{array}{c}x=-\frac{b}{2a}=3\\ y=9a+3b+3=-2\end{array}\right.\iff \left\{\begin{array}{c}6a+b=0\\ 9a+3b=-5\end{array}\right.\iff \left\{\begin{array}{c}a=\frac{5}{9}\\ b=-\frac{10}{3}\end{array}\right.$

   Suy ra phương trình của Parabol (P) là $y=\frac{5}{9}{x}^2-\frac{10}{3}x+3$

   Đáp án cần chọn là: D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Xác định Parabol (P): y=ax2+bx−5 biết rằng Parabol đi qua điểm A(3;−4) và có trục đối xứng x = −32
   
   

   Câu hỏi:
   

   Xác định Parabol (P): $y=a{x}^2+bx-5$ biết rằng Parabol đi qua điểm A(3;−4) và có trục đối xứng x = −$\frac{3}{2}$

   A. $y=\frac{1}{18}{x}^2+\frac{1}{6}x-5$

   Đáp án chính xác

   B. $y=\frac{1}{18}{x}^2+\frac{1}{6}x+5$

   C. $y=3x^2+9x-9$

   D. $y=-\frac{1}{18}{x}^2+\frac{1}{6}x-5$

   Trả lời:

   (P) đi qua điểm A(3;−4) nên $-4=9a+3b-5\iff 9a+3b=1$

   Trục đối xứng $x=-\frac{b}{2a}=-\frac{3}{2}\iff b=3a$

   Suy ra hệ phương trình $\left\{\begin{array}{c}9a+3b=1\\ 3a-b=0\end{array}\right.\iff \left\{\begin{array}{c}a=\frac{1}{18}\\ b=\frac{1}{6}\end{array}\right.$

   Vậy phương trình của (P)là $y=\frac{1}{18}{x}^2+\frac{1}{6}x-5$

   Đáp án cần chọn là: A

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tìm các giá trị của tham số m để phương trình 2×2−2x+1−m=0  có hai nghiệm phân biệt
   
   

   Câu hỏi:
   

   Tìm các giá trị của tham số m để phương trình $2x^2-2x+1-m=0$ có hai nghiệm phân biệt

   A. $m>\frac{1}{2}$

   Đáp án chính xác

   B. $m=\frac{1}{2}$

   C. $m<\frac{1}{2}$

   D. Không tồn tại

   Trả lời:

   $2x^2-2x+1-m=0\iff 2x^2-2x=m-1$
   Số nghiệm của phương trình đã cho bằng số giao điểm của Parabol
   $\left(P\right):y=2x^2-2x$ và đường thẳng $y=m-1$ có tính chất song song với trục hoành.
   Parabol (P) có tọa độ đỉnh $\left(-\frac{b}{2a};-\frac{\text{Δ}}{4a}\right)=\left(\frac{1}{2};-\frac{1}{2}\right)$
   
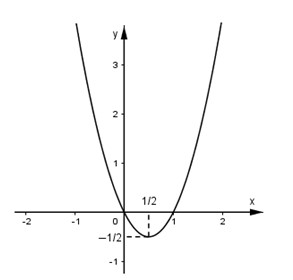
   Dựa trên đồ thị ta thấy phương trình đã cho có hai nghiệm khi và chỉ khi
   $m-1>-\frac{1}{2}\iff m>\frac{1}{2}$

   Đáp án cần chọn là: A

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hàm số f(x)=x2+2x−3  Xét các mệnh đề sau:  (i) f(x−1)=x2−4 (ii) Hàm số đã cho đồng biến trên −1;+∞ (iii) Giá trị nhỏ nhất của hàm số là một số âm. (iv) Phương trình f(x)=m có nghiệm khi m≥−4 Số mệnh đề đúng là:
   
   

   Câu hỏi:
   

   Cho hàm số $f\left(x\right)=x^2+2x-3$ 

   Xét các mệnh đề sau: 
   (i) $f(x-1)=x^2-4$
   (ii) Hàm số đã cho đồng biến trên $\left(-1;+\infty \right)$
   (iii) Giá trị nhỏ nhất của hàm số là một số âm.
   (iv) Phương trình $f\left(x\right)=m$có nghiệm khi $m\ge -4$

   Số mệnh đề đúng là:

   A. 1

   B. 2

   C. 3

   D. 4

   Đáp án chính xác

   Trả lời:

   Ta có $f\left(x-1\right)={\left(x-1\right)}^2+2\left(x-1\right)-3=x^2-4$
   Với trục đối xứng $x=-\frac{b}{2a}=-1$ và hệ số $a=1>0$ thì hàm số đồng biến trên $\left(-1;+\infty \right)$
   Biến đối $f\left(x\right)=x^2+2x-3={\left(x+1\right)}^2-4\ge -4$ ⇒ GTNN của hàm số là −4 < 0
   Dễ thấy $f\left(x\right)=m\iff {\left(x+1\right)}^2=m+4$ nên để phương trình có nghiệm thì
   $m+4\ge 0\iff m\ge -4$

   Đáp án cần chọn là: D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tìm các giá trị của m để hàm số y=x2+mx+5 luôn đồng biến trên 1;+∞
   
   

   Câu hỏi:
   

   Tìm các giá trị của m để hàm số $y=x^2+mx+5$luôn đồng biến trên $\left(1;+\infty \right)$

   A. m < −2

   B. m ≥ −2

   Đáp án chính xác

   C. m = −4

   D. Không xác định được

   Trả lời:

   Trục đối xứng $x=-\frac{b}{2a}=-\frac{m}{2}$

   Với hệ số a = 1 > 0 thì hàm số đã cho đồng biến trên $\left(-\frac{m}{2};+\infty \right)$
   Vậy để hàm số luôn đồng biến trên $\left(1;+\infty \right)$ thì $-\frac{m}{2}\le 1\iff m\ge -2$

   Đáp án cần chọn là: B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====