Câu hỏi:
Tìm các giá trị của m để phương trình \({x^2} – 2x + \sqrt {4{x^2} – 12x + 9} = m\) có nghiệm duy nhất.
A.\( – \frac{3}{4} < m < 0\)
B. \( – \frac{{\sqrt 3 }}{2} < m < \frac{{\sqrt 3 }}{2}\)
C. \(m = – \frac{3}{4}\)
Đáp án chính xác
D. Không tồn tại
Trả lời:
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số
\(y = {x^2} – 2x + \left| {2x – 3} \right|\)và đường thẳng y = m có tính chất song song với trục hoành.
Đồ thị hàm số \(y = {x^2} – 2x + |2x – 3|\)
\( = \left\{ {\begin{array}{*{20}{c}}{{x^2} – 2x + 2x – 3 = {x^2} – 3({P_1})\,khi\,x \ge \frac{3}{2}}\\{{x^2} – 2x – 2x + 3 = {x^2} – 4x + 3({P_2})\,khi\,x < \frac{3}{2}}\end{array}} \right.\)
được vẽ như sau:
+ Vẽ lần lượt hai đồ thị hàm số trên cùng một hệ trục tọa độ
+ Xóa đi nhánh bên trái điểm \(x = \frac{3}{2}\) của đồ thị hàm số \(y = {x^2} – 3\)
+ Xóa đi nhánh bên phải điểm \(x = \frac{3}{2}\)của đồ thị hàm số \(y = {x^2} – 4x + 3\)
Tọa độ giao điểm của đồ thị hàm số (P1) và (P2) là \(\left( {\frac{3}{2}; – \frac{3}{4}} \right)\)
Dựa trên đồ thị ta thấy phương trình đã cho có nghiệm duy nhất khi và chỉ khi \(m = – \frac{3}{4}\)
Đáp án cần chọn là: C
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho đồ thị hàm số \(y = a{x^2} + bx + c\) như hình vẽ.
Khẳng định nào sau đây là đúng: – ĐGNL-HN
Câu hỏi:
Cho đồ thị hàm số \(y = a{x^2} + bx + c\) như hình vẽ.
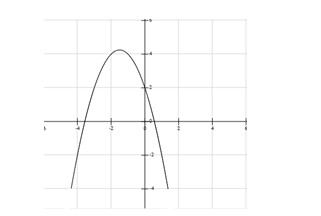
Khẳng định nào sau đây là đúng:A.a >0, b < 0, c >0
B. a < 0, b >0,c >0
C. a < 0, b < 0, c < 0
D. a < 0, b < 0, c >0
Đáp án chính xác
Trả lời:
Bề lõm của đồ thị quay xuống dưới nên hệ số a < 0.
Giao điểm của đồ thị hàm số với trục tung nằm trên trục có tung độ dương nên c >0
Hoành độ đỉnh \(x = – \frac{b}{{2a}} < 0\) Mà a < 0 nên b < 0.
Đáp án cần chọn là: D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Xác định Parabol (P):\(y = a{x^2} + bx + 2\;\) biết rằng Parabol đi qua hai điểm M(1;5) và N(2;−2). – ĐGNL-HN
Câu hỏi:
Xác định Parabol (P):\(y = a{x^2} + bx + 2\;\) biết rằng Parabol đi qua hai điểm M(1;5) và N(2;−2).
A.\(y = – 5{x^2} + 8x + 2\)
Đáp án chính xác
B. \(y = 10{x^2} + 13x + 2\)
C. \(y = – 10{x^2} – 13x + 2\)
D. \(y = 9{x^2} + 6x – 5\)
Trả lời:
Vì \(M,\,\,N \in (P)\) nên tọa độ của hai điểm M, N phải thỏa mãn phương trình của (P).
Do đó, ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{5 = a + b + 2}\\{ – 2 = 4a + 2b + 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = – 5}\\{b = 8}\end{array}} \right.\)
Vậy phương trình của (P)là:\(y = – 5{x^2} + 8x + 2\)
Đáp án cần chọn là: A====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Xác định Parabol (P):\(y = a{x^2} + bx – 5\) biết rằng Parabol đi qua điểm A(3;−4) và có trục đối xứng x = −\(\frac{3}{2}\). – ĐGNL-HN
Câu hỏi:
Xác định Parabol (P):\(y = a{x^2} + bx – 5\) biết rằng Parabol đi qua điểm A(3;−4) và có trục đối xứng x = −\(\frac{3}{2}\).
A.\(y = \frac{1}{{18}}{x^2} + \frac{1}{6}x – 5\)
Đáp án chính xác
B. \(y = \frac{1}{{18}}{x^2} + \frac{1}{6}x + 5\)
C. \(y = 3{x^2} + 9x – 9\)
D. \(y = – \frac{1}{{18}}{x^2} + \frac{1}{6}x – 5\)
Trả lời:
(P) đi qua điểm A(3;−4) nên \( – 4 = 9a + 3b – 5 \Leftrightarrow 9a + 3b = 1\).
Trục đối xứng \(x = – \frac{b}{{2a}} = – \frac{3}{2} \Leftrightarrow b = 3a\)
Suy ra hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{9a + 3b = 1}\\{3a – b = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{1}{{18}}}\\{b = \frac{1}{6}}\end{array}} \right.\)
Vậy phương trình của (P)là:\(y = \frac{1}{{18}}{x^2} + \frac{1}{6}x – 5\)
Đáp án cần chọn là: A====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Xác định Parabol (P):\(y = a{x^2} + bx + 3\;\) biết rằng Parabol có đỉnh I(3;−2). – ĐGNL-HN
Câu hỏi:
Xác định Parabol (P):\(y = a{x^2} + bx + 3\;\) biết rằng Parabol có đỉnh I(3;−2).
A.\(y = {x^2} – 6x + 3\)
B. \(y = – \frac{5}{9}{x^2} + \frac{{10}}{3}x + 3\)
C. \(y = 3{x^2} + 9x + 3\)
D. \(y = \frac{5}{9}{x^2} – \frac{{10}}{3}x + 3\)
Đáp án chính xác
Trả lời:
Ta có đỉnh của (P)có tọa độ
\(\left\{ {\begin{array}{*{20}{c}}{x = – \frac{b}{{2a}} = 3}\\{y = 9a + 3b + 3 = – 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{6a + b = 0}\\{9a + 3b = – 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{5}{9}}\\{b = – \frac{{10}}{3}}\end{array}} \right.\)
Suy ra phương trình của Parabol (P)là:\(y = \frac{5}{9}{x^2} – \frac{{10}}{3}x + 3\)
Đáp án cần chọn là: D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Viết phương trình của Parabol (P) biết rằng (P) đi qua các điểm A(0;2),B(−2;5),C(3;8) – ĐGNL-HN
Câu hỏi:
Viết phương trình của Parabol (P) biết rằng (P) đi qua các điểm A(0;2),B(−2;5),C(3;8)
A.\(\)\(y = \frac{7}{{10}}{x^2} + \frac{1}{{10}}x – 2\)
B. \(y = \frac{7}{{10}}{x^2} – \frac{1}{{10}}x + 2\)
Đáp án chính xác
C. \(y = \frac{7}{{10}}{x^2} – \frac{1}{{10}}x – 2\)
D. \(y = \frac{7}{{10}}{x^2} + \frac{1}{{10}}x + 2\)
Trả lời:
Phương trình (P) có dạng \(y = a{x^2} + bx + c\,\,\,\,\left( {a \ne 0} \right)\)
Ba điểm A,B,C thuộc (P) nên tọa độ của chúng phải thỏa mãn phương trình (P)
Do đó, ta có hệ phương trình\(\left\{ {\begin{array}{*{20}{c}}{2 = a{{.0}^2} + b.0 + c}\\{5 = a.{{( – 2)}^2} + b.( – 2) + c}\\{8 = a{{.3}^2} + b.3 + c}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{7}{{10}}}\\{b = – \frac{1}{{10}}}\\{c = 2}\end{array}} \right.\)
Suy ra phương trình của (P) là: \(y = \frac{7}{{10}}{x^2} – \frac{1}{{10}}x + 2\)Đáp án cần chọn là: B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
