Câu hỏi:
Cho phương trình của (P):\(y = a{x^2} + bx + c\left( {a \ne 0} \right)\) biết rằng hàm số có giá trị lớn nhất bằng 1 và đồ thị hàm số đi qua các điểm A(2;0), B(−2;−8) Tình tổng \({a^2} + {b^2} + {c^2}\)
A.\({a^2} + {b^2} + {c^2} = 3\)
B. \({a^2} + {b^2} + {c^2} = \frac{{29}}{{16}}\)
C. \({a^2} + {b^2} + {c^2} = \frac{{48}}{{29}}\)
D. \(\left[ {\begin{array}{*{20}{c}}{{a^2} + {b^2} + {c^2} = 5}\\{{a^2} + {b^2} + {c^2} = \frac{{209}}{{16}}}\end{array}} \right.\)
Đáp án chính xác
Trả lời:
Dễ thấy rằng đồ thị của (P) có đỉnh đặt trên đường thẳng y = 1 và hệ số m < 0..
Do đó, phương trình của (P) có dạng \(y = m{\left( {x – u} \right)^2} + 1\,\,(m < 0)\)(P) đi qua các điểm A(2;0), B(−2;−8) nên có hệ phương trình
\(\left\{ {\begin{array}{*{20}{c}}{m{{(2 – u)}^2} + 1 = 0}\\{m{{( – 2 – u)}^2} + 1 = – 8}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}}{m = – \frac{1}{{{{(2 – u)}^2}}}}\\{m = – \frac{9}{{{{( – 2 – u)}^2}}}}\end{array}} \right. \Rightarrow \Rightarrow – \frac{1}{{{{\left( {2 – u} \right)}^2}}} = – \frac{9}{{{{\left( { – 2 – u} \right)}^2}}}\)
\( \Rightarrow {\left( {u + 2} \right)^2} = 9{\left( {2 – u} \right)^2} \Leftrightarrow 8{u^2} – 40u + 32 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{u = 1}\\{u = 4}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{u = 1}\\{m = – 1\left( {tm} \right)}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{u = 4}\\{m = – \frac{1}{4}\left( {tm} \right)}\end{array}} \right.}\end{array}} \right.\)
Từ đây có hai phương trình (P) thỏa mãn là\(y = – {x^2} + 2x,\,\,\,y = – \frac{1}{4}{x^2} + 2x – 3\)
Suy ra \({a^2} + {b^2} + {c^2} = 5\) hoặc \({a^2} + {b^2} + {c^2} = \frac{{209}}{{16}}\)
Đáp án cần chọn là: D
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho đồ thị hàm số \(y = a{x^2} + bx + c\) như hình vẽ.
Khẳng định nào sau đây là đúng: – ĐGNL-HN
Câu hỏi:
Cho đồ thị hàm số \(y = a{x^2} + bx + c\) như hình vẽ.
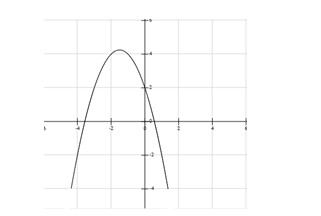
Khẳng định nào sau đây là đúng:A.a >0, b < 0, c >0
B. a < 0, b >0,c >0
C. a < 0, b < 0, c < 0
D. a < 0, b < 0, c >0
Đáp án chính xác
Trả lời:
Bề lõm của đồ thị quay xuống dưới nên hệ số a < 0.
Giao điểm của đồ thị hàm số với trục tung nằm trên trục có tung độ dương nên c >0
Hoành độ đỉnh \(x = – \frac{b}{{2a}} < 0\) Mà a < 0 nên b < 0.
Đáp án cần chọn là: D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Xác định Parabol (P):\(y = a{x^2} + bx + 2\;\) biết rằng Parabol đi qua hai điểm M(1;5) và N(2;−2). – ĐGNL-HN
Câu hỏi:
Xác định Parabol (P):\(y = a{x^2} + bx + 2\;\) biết rằng Parabol đi qua hai điểm M(1;5) và N(2;−2).
A.\(y = – 5{x^2} + 8x + 2\)
Đáp án chính xác
B. \(y = 10{x^2} + 13x + 2\)
C. \(y = – 10{x^2} – 13x + 2\)
D. \(y = 9{x^2} + 6x – 5\)
Trả lời:
Vì \(M,\,\,N \in (P)\) nên tọa độ của hai điểm M, N phải thỏa mãn phương trình của (P).
Do đó, ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{5 = a + b + 2}\\{ – 2 = 4a + 2b + 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = – 5}\\{b = 8}\end{array}} \right.\)
Vậy phương trình của (P)là:\(y = – 5{x^2} + 8x + 2\)
Đáp án cần chọn là: A====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Xác định Parabol (P):\(y = a{x^2} + bx – 5\) biết rằng Parabol đi qua điểm A(3;−4) và có trục đối xứng x = −\(\frac{3}{2}\). – ĐGNL-HN
Câu hỏi:
Xác định Parabol (P):\(y = a{x^2} + bx – 5\) biết rằng Parabol đi qua điểm A(3;−4) và có trục đối xứng x = −\(\frac{3}{2}\).
A.\(y = \frac{1}{{18}}{x^2} + \frac{1}{6}x – 5\)
Đáp án chính xác
B. \(y = \frac{1}{{18}}{x^2} + \frac{1}{6}x + 5\)
C. \(y = 3{x^2} + 9x – 9\)
D. \(y = – \frac{1}{{18}}{x^2} + \frac{1}{6}x – 5\)
Trả lời:
(P) đi qua điểm A(3;−4) nên \( – 4 = 9a + 3b – 5 \Leftrightarrow 9a + 3b = 1\).
Trục đối xứng \(x = – \frac{b}{{2a}} = – \frac{3}{2} \Leftrightarrow b = 3a\)
Suy ra hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{9a + 3b = 1}\\{3a – b = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{1}{{18}}}\\{b = \frac{1}{6}}\end{array}} \right.\)
Vậy phương trình của (P)là:\(y = \frac{1}{{18}}{x^2} + \frac{1}{6}x – 5\)
Đáp án cần chọn là: A====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Xác định Parabol (P):\(y = a{x^2} + bx + 3\;\) biết rằng Parabol có đỉnh I(3;−2). – ĐGNL-HN
Câu hỏi:
Xác định Parabol (P):\(y = a{x^2} + bx + 3\;\) biết rằng Parabol có đỉnh I(3;−2).
A.\(y = {x^2} – 6x + 3\)
B. \(y = – \frac{5}{9}{x^2} + \frac{{10}}{3}x + 3\)
C. \(y = 3{x^2} + 9x + 3\)
D. \(y = \frac{5}{9}{x^2} – \frac{{10}}{3}x + 3\)
Đáp án chính xác
Trả lời:
Ta có đỉnh của (P)có tọa độ
\(\left\{ {\begin{array}{*{20}{c}}{x = – \frac{b}{{2a}} = 3}\\{y = 9a + 3b + 3 = – 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{6a + b = 0}\\{9a + 3b = – 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{5}{9}}\\{b = – \frac{{10}}{3}}\end{array}} \right.\)
Suy ra phương trình của Parabol (P)là:\(y = \frac{5}{9}{x^2} – \frac{{10}}{3}x + 3\)
Đáp án cần chọn là: D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Viết phương trình của Parabol (P) biết rằng (P) đi qua các điểm A(0;2),B(−2;5),C(3;8) – ĐGNL-HN
Câu hỏi:
Viết phương trình của Parabol (P) biết rằng (P) đi qua các điểm A(0;2),B(−2;5),C(3;8)
A.\(\)\(y = \frac{7}{{10}}{x^2} + \frac{1}{{10}}x – 2\)
B. \(y = \frac{7}{{10}}{x^2} – \frac{1}{{10}}x + 2\)
Đáp án chính xác
C. \(y = \frac{7}{{10}}{x^2} – \frac{1}{{10}}x – 2\)
D. \(y = \frac{7}{{10}}{x^2} + \frac{1}{{10}}x + 2\)
Trả lời:
Phương trình (P) có dạng \(y = a{x^2} + bx + c\,\,\,\,\left( {a \ne 0} \right)\)
Ba điểm A,B,C thuộc (P) nên tọa độ của chúng phải thỏa mãn phương trình (P)
Do đó, ta có hệ phương trình\(\left\{ {\begin{array}{*{20}{c}}{2 = a{{.0}^2} + b.0 + c}\\{5 = a.{{( – 2)}^2} + b.( – 2) + c}\\{8 = a{{.3}^2} + b.3 + c}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{7}{{10}}}\\{b = – \frac{1}{{10}}}\\{c = 2}\end{array}} \right.\)
Suy ra phương trình của (P) là: \(y = \frac{7}{{10}}{x^2} – \frac{1}{{10}}x + 2\)Đáp án cần chọn là: B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
