Câu hỏi:
Cho tứ diện ABCD có AB=CD=4,BC=AD=5,AC=BD=6. M là điểm thay đổi trong tâm giác ABC. Các đường thẳng qua M song song với AD,BD,CD tương ứng cắt mặt phẳng (BCD),(ACD),(ABD) tại A′,B′,C′. Giá trị lớn nhất của MA′.MB′.MC′ là
A.\(\frac{{40}}{9}\)
Đáp án chính xác
B. \(\frac{{24}}{9}\)
C. \(\frac{{30}}{9}\)
D. \(\frac{{20}}{9}\)
Trả lời:
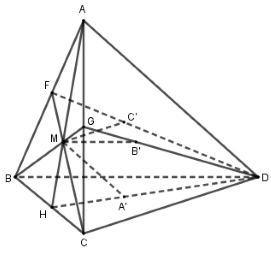
Trong tam giác ABC, kéo dài AM,BM,CM cắt các đoạn thẳng BC,CA,AB lần lượt tại H,G,F.
+) Trong mặt phẳng (HAD), kẻ MA′//AD.
+) Trong mặt phẳng (GBD), kẻ MB′//BD.
+) Trong mặt phẳng (FCD), kẻ MC′//CD.
Từ đó ta được các điểm A′,B′,C′ cần tìm.
Theo định lý Ta – let ta có: \(\frac{{MA’}}{{AD}} = \frac{{HM}}{{HA}} \Rightarrow MA’ = 5.\frac{{MH}}{{AH}}\)
\(\frac{{MB’}}{{BD}} = \frac{{GM}}{{GB}} \Rightarrow MB’ = 6.\frac{{MG}}{{BG}};\frac{{MC’}}{{CD}} = \frac{{FM}}{{FC}} \Rightarrow MC’ = 4.\frac{{MF}}{{CF}}\)
\( \Rightarrow MA’.MB’.MC’ = 120.\frac{{MH}}{{AH}}.\frac{{MG}}{{BG}}.\frac{{MF}}{{CF}}\)
Trong tam giác ABC ta có:\(1 = \frac{{MH}}{{AH}} + \frac{{MG}}{{BG}} + \frac{{MF}}{{CF}} \ge 3\sqrt[3]{{\frac{{MH}}{{AH}}.\frac{{MG}}{{BG}}.\frac{{MF}}{{CF}}}}\)
\( \Rightarrow \frac{{MH}}{{AH}}.\frac{{MG}}{{BG}}.\frac{{MF}}{{CF}} \le \frac{1}{{27}}\)
Do đó\(MA’.MB’.MC’ = 120.\frac{{MH}}{{AH}}.\frac{{MG}}{{BG}}.\frac{{MF}}{{CF}} \le 120.\frac{1}{{27}} = \frac{{40}}{9}\)
\( \Rightarrow {\left( {MA’.MB’.MC’} \right)_{\max }} = \frac{{40}}{9}\)
Đáp án cần chọn là: A
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số điểm chung của đường thẳng và mặt phẳng không thể là: – ĐGNL-HN
Câu hỏi:
Số điểm chung của đường thẳng và mặt phẳng không thể là:
A.chỉ hai điểm
Đáp án chính xác
B.một điểm
C.không có điểm nào
D.vô số điểm
Trả lời:
Đường thẳng và mặt phẳng nếu có hai điểm chung thì sẽ có vô số điểm chung nên không thể chỉ có hai điểm chung.Đáp án cần chọn là: A
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Nếu đường thẳng d và mặt phẳng (α) không có điểm chung thì chúng – ĐGNL-HN
Câu hỏi:
Nếu đường thẳng d và mặt phẳng (α) không có điểm chung thì chúng
A.song song
Đáp án chính xác
B.cắt nhau
C.chéo nhau
D.trùng nhau
Trả lời:
Nếu đường thẳng d và mặt phẳng (α) không có điểm chung thì chúng song song.Đáp án cần chọn là: A
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho đường thẳng d và mặt phẳng (α) như hình vẽ, số điểm chung của d và (α) là: – ĐGNL-HN
Câu hỏi:
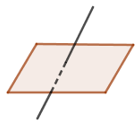
Cho đường thẳng d và mặt phẳng (α) như hình vẽ, số điểm chung của d và (α) là:
A.0
B.1
Đáp án chính xác
C.2
D.vô số
Trả lời:
Từ hình vẽ ta thấy d cắt (α) tại duy nhất một điểm.Đáp án cần chọn là: B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tứ diện ABCD. Chọn kết luận đúng: – ĐGNL-HN
Câu hỏi:
Cho tứ diện ABCD. Chọn kết luận đúng:
A.\(AD \subset \left( {ABC} \right)\)
b.\(AD \cap \left( {ABC} \right) = C\)
c.\(AB \subset \left( {ABC} \right)\)
Đáp án chính xác
d.\(AC//\left( {ABD} \right)\)
Trả lời:
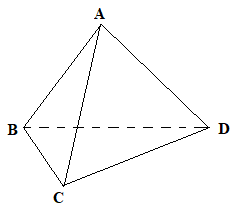
Từ hình vẽ ta thấy:
+) Đường thẳng AD cắt mặt phẳng (ABC) tại điểm duy nhất A nên đáp án A, B đều sai.
\( + )A \in \left( {ABC} \right),B \in \left( {ABC} \right) \Rightarrow AB \subset \left( {ABC} \right)\) nên C đúng.
+) Đường thẳng AC cắt mặt phẳng (ABD) tại điểm duy nhất A nên D sai.Đáp án cần chọn là: C
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Nếu một đường thẳng d không nằm trong mặt phẳng (α) mà nó song song với đường thẳng d′ trong (α) thì: – ĐGNL-HN
Câu hỏi:
Nếu một đường thẳng d không nằm trong mặt phẳng (α) mà nó song song với đường thẳng d′ trong (α) thì:
A.\(d//(\alpha )\;\)
Đáp án chính xác
B.d cắt \(\left( \alpha \right)\;\)
C. \(d \subset \left( \alpha \right)\)
D. \(d \supset \left( \alpha \right)\)
Trả lời:
Nếu đường thẳng d không nằm trong mặt phẳng (α) mà d song song với một đường thẳng d′ nằm trong (α) thì d song song với (α).
Đáp án cần chọn là: A====== **** mời các bạn xem câu tiếp bên dưới **** =====
