Câu hỏi:
Cho hình chóp S.ABC, M là một điểm nằm trong tam giác ABC. Các đường thẳng qua MM và song song với SA,SB,SC cắt các mặt (SBC),(SAC),(SAB) lần lượt tại A′,B′,C′. \(\frac{{MA’}}{{SA}} + \frac{{MB’}}{{SB}} + \frac{{MC’}}{{SC}}\) có giá trị không đổi bằng bao nhiêu khi M di động trong tam giác ABC?
A.\(\frac{1}{3}\)
B. \(\frac{1}{2}\)
C. 1
Đáp án chính xác
D. \(\frac{2}{3}\)
Trả lời:
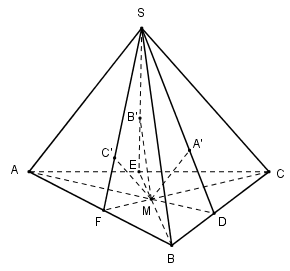
Trong (SAD) ta kẻ đường thẳng qua M và song song với SA cắt (SBC) tại A′.A′.
Trong (SCF) kẻ đường thẳng qua M và song song với SC cắt SF tại C′
\(MA’//SA \Rightarrow \frac{{MA’}}{{SA}} = \frac{{DM}}{{DA}} = \frac{{{S_{MBC}}}}{{{S_{ABC}}}}\)
Tương tự ta chứng minh được \(\frac{{MB’}}{{SB}} = \frac{{EM}}{{EB}} = \frac{{{S_{MAC}}}}{{{S_{ABC}}}}\) và\(\frac{{MC’}}{{SC}} = \frac{{FM}}{{FC}} = \frac{{{S_{MAB}}}}{{{S_{ABC}}}}\)
Do đó ta có: \(\frac{{MA’}}{{SA}} + \frac{{MB’}}{{SB}} + \frac{{MC’}}{{SC}} = \frac{{{S_{MBC}}}}{{{S_{ABC}}}} + \frac{{{S_{MAC}}}}{{{S_{ABC}}}} + \frac{{{S_{MAB}}}}{{{S_{ABC}}}} = 1\)
Đáp án cần chọn là: C
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số điểm chung của đường thẳng và mặt phẳng không thể là: – ĐGNL-HN
Câu hỏi:
Số điểm chung của đường thẳng và mặt phẳng không thể là:
A.chỉ hai điểm
Đáp án chính xác
B.một điểm
C.không có điểm nào
D.vô số điểm
Trả lời:
Đường thẳng và mặt phẳng nếu có hai điểm chung thì sẽ có vô số điểm chung nên không thể chỉ có hai điểm chung.Đáp án cần chọn là: A
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Nếu đường thẳng d và mặt phẳng (α) không có điểm chung thì chúng – ĐGNL-HN
Câu hỏi:
Nếu đường thẳng d và mặt phẳng (α) không có điểm chung thì chúng
A.song song
Đáp án chính xác
B.cắt nhau
C.chéo nhau
D.trùng nhau
Trả lời:
Nếu đường thẳng d và mặt phẳng (α) không có điểm chung thì chúng song song.Đáp án cần chọn là: A
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho đường thẳng d và mặt phẳng (α) như hình vẽ, số điểm chung của d và (α) là: – ĐGNL-HN
Câu hỏi:
Cho đường thẳng d và mặt phẳng (α) như hình vẽ, số điểm chung của d và (α) là:
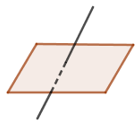
A.0
B.1
Đáp án chính xác
C.2
D.vô số
Trả lời:
Từ hình vẽ ta thấy d cắt (α) tại duy nhất một điểm.Đáp án cần chọn là: B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tứ diện ABCD. Chọn kết luận đúng: – ĐGNL-HN
Câu hỏi:
Cho tứ diện ABCD. Chọn kết luận đúng:
A.\(AD \subset \left( {ABC} \right)\)
b.\(AD \cap \left( {ABC} \right) = C\)
c.\(AB \subset \left( {ABC} \right)\)
Đáp án chính xác
d.\(AC//\left( {ABD} \right)\)
Trả lời:
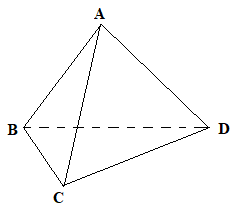
Từ hình vẽ ta thấy:
+) Đường thẳng AD cắt mặt phẳng (ABC) tại điểm duy nhất A nên đáp án A, B đều sai.
\( + )A \in \left( {ABC} \right),B \in \left( {ABC} \right) \Rightarrow AB \subset \left( {ABC} \right)\) nên C đúng.
+) Đường thẳng AC cắt mặt phẳng (ABD) tại điểm duy nhất A nên D sai.Đáp án cần chọn là: C
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Nếu một đường thẳng d không nằm trong mặt phẳng (α) mà nó song song với đường thẳng d′ trong (α) thì: – ĐGNL-HN
Câu hỏi:
Nếu một đường thẳng d không nằm trong mặt phẳng (α) mà nó song song với đường thẳng d′ trong (α) thì:
A.\(d//(\alpha )\;\)
Đáp án chính xác
B.d cắt \(\left( \alpha \right)\;\)
C. \(d \subset \left( \alpha \right)\)
D. \(d \supset \left( \alpha \right)\)
Trả lời:
Nếu đường thẳng d không nằm trong mặt phẳng (α) mà d song song với một đường thẳng d′ nằm trong (α) thì d song song với (α).
Đáp án cần chọn là: A====== **** mời các bạn xem câu tiếp bên dưới **** =====
