Giải phương trình cosx+cos3x+2cos5x=0

Câu hỏi:

Giải phương trình $\cos x+\cos 3x+2\cos 5x=0$

A. $x=\frac{\pi }{2}+k\pi ,x=\pm \frac{1}{5}\arccos \frac{1+\sqrt{17}}{8}+k\pi ,x=\pm \frac{1}{5}\arccos \frac{1-\sqrt{17}}{8}+k\pi$

B. $x=\pm \frac{\pi }{6}+k\pi$

C. $x=\pm \frac{1}{2}\arccos \frac{1+\sqrt{15}}{7}+k\pi ,x=\pm \frac{1}{2}\arccos \frac{1-\sqrt{15}}{7}+k\pi$

D. $x=\frac{\pi }{2}+k\pi ,x=\pm \frac{1}{2}\arccos \frac{1+\sqrt{17}}{8}+k\pi ,x=\pm \frac{1}{2}\arccos \frac{1-\sqrt{17}}{8}+k\pi$

Đáp án chính xác

Trả lời:

cosx + cos3x + 2cos5x = 0
⇔ cosx + cos3x + cos5x + cos5x = 0
⇔ (cosx + cos5x) + (cos3x + cos5x) = 0
⇔ 2cos3xcos2x + 2cos4xcosx = 0
⇔ 2(4cos³ x − 3cosx)cos2x + 2cos4xcosx = 0
⇔2cosx(4cos² x − 3)cos2x + 2cos4xcosx = 0
⇔ 2cosx[(4cos² x − 3)cos2x + cos4x] = 0
⇔ 2cosx[[2(1 + cos2x) − 3]cos2x + 2cos² 2x − 1] = 0
⇔ 2cosx[(2cos2x − 1)cos2x + 2cos² 2x − 1] = 0
⇔ 2cosx[4cos² 2x − cos2x − 1] = 0
$\iff \left[\begin{array}{c}\cos x=0\\ \cos 2x=\frac{1+\sqrt{17}}{8}\\ \cos 2x=\frac{1-\sqrt{17}}{8}\end{array}\right.$
$\iff \left[\begin{array}{c}x=\frac{\pi }{2}+k\pi \\ 2x=\pm \arccos \frac{1+\sqrt{17}}{8}+k2\pi \\ 2x=\pm \arccos \frac{1-\sqrt{17}}{8}+k2\pi \end{array}\right.$
$\iff \left[\begin{array}{c}x=\frac{\pi }{2}+k\pi \\ x=\pm \frac{1}{2}\arccos \frac{1+\sqrt{17}}{8}+k\pi \\ x=\pm \frac{1}{2}\arccos \frac{1-\sqrt{17}}{8}+k\pi \end{array}\right.$
 
Vậy nghiệm của phương trình là: $x=\frac{\pi }{2}+k\pi ,x=\pm \frac{1}{2}\arccos \frac{1+\sqrt{17}}{8}+k\pi ,x=\pm \frac{1}{2}\arccos \frac{1-\sqrt{17}}{8}+k\pi$
Đáp án cần chọn là: D

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Phương trình sin2x+3sin4x=0 có nghiệm là:
   
   

   Câu hỏi:
   

   Phương trình $\sin 2x+3\sin 4x=0$ có nghiệm là:

   A. $\left[\begin{array}{c}x=\frac{k\pi }{2}\\ x=\pm \frac{1}{2}\arccos \left(-\frac{1}{6}\right)+k\pi \end{array}\right.\left(k\in Z\right)$

   Đáp án chính xác

   B. $\left[\begin{array}{c}x=\frac{k\pi }{2}\\ x=\pm \frac{5}{2}\arccos \left(-\frac{1}{6}\right)+k\pi \end{array}\right.\left(k\in Z\right)$

   C. $\left[\begin{array}{c}x=\frac{k\pi }{2}\\ x=\pm \frac{1}{2}\arccos \left(-\frac{1}{3}\right)+k\pi \end{array}\right.\left(k\in Z\right)$

   D. $\left[\begin{array}{c}x=\frac{k\pi }{2}\\ x=\pm \frac{1}{3}\arccos \left(-\frac{1}{6}\right)+k\pi \end{array}\right.\left(k\in Z\right)$

   Trả lời:

   $\sin 2x+3\sin 4x=0$
   $\iff \sin 2x+6\sin 2x\cos 2x=0$
   $\iff \sin 2x\left(1+6\cos 2x\right)=0$
   $\iff \left[\begin{array}{c}\sin 2x=0\\ 1+6\cos 2x=0\end{array}\right.$
   $\iff \left[\begin{array}{c}\sin 2x=0\\ \cos 2x=-\frac{1}{6}\end{array}\right.$
   $\iff \left[\begin{array}{c}2x=k\pi \\ 2x=\pm \arccos \left(-\frac{1}{6}\right)+k2\pi \end{array}\right.$
   $\iff \left[\begin{array}{c}x=\frac{k\pi }{2}\\ x=\pm \frac{1}{2}\arccos \left(-\frac{1}{6}\right)+k\pi \end{array}\right.\left(k\in Z\right)$
    
   Đáp án cần chọn là: A

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Phương trình cos2x1−sin2x=0 có nghiệm là:
   
   

   Câu hỏi:
   

   Phương trình $\frac{\cos 2x}{1-\sin 2x}=0$ có nghiệm là:

   A. $x=\frac{\pi }{4}+k\pi \left(k\in Z\right)$

   B. $x=\frac{\pi }{4}+\frac{k\pi }{2}\left(k\in Z\right)$

   C. $x=\frac{3\pi }{4}+2k\pi \left(k\in Z\right)$

   D. $x=\frac{3\pi }{4}+k\pi \left(k\in Z\right)$

   Đáp án chính xác

   Trả lời:

   Bước 1:
   Điều kiện:$1-\sin 2x\ne 0$
   $\iff \sin 2x\ne 1$
   $\iff 2x\ne \frac{\pi }{2}+k2\pi$
   $\iff x\ne \frac{\pi }{4}+k\pi \left(k\in Z\right)$
   Bước 2:
   $\frac{\cos 2x}{1-\sin 2x}=0$
   $\iff \cos 2x=0$
   $\iff {\cos }^{2}2x=0$
   $\iff 1-si{n}^{2}2x=0$
   $\iff si{n}^{2}2x=1$
   $\iff sin2x=-1\left(do\sin 2x\ne 1\right)$
   $\iff 2x=-\frac{\pi }{2}+k2\pi$
   $\iff x=-\frac{\pi }{4}+k\pi$
   Đặt k = l + 1 ta được:
   $-\frac{\pi }{4}+k\pi =-\frac{\pi }{4}+l\pi +\pi =\frac{3\pi }{4}+l\pi \left(l\in Z\right)$
   Vậy $\left[\begin{array}{c}x=\frac{3\pi }{4}+l\pi \left(l\in Z\right)\\ x=\frac{3\pi }{4}+k\pi \left(k\in Z\right)\end{array}\right.$
   Đáp án cần chọn là: D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Phương trình 3cot2x−4cotx+3=0 có nghiệm là:
   
   

   Câu hỏi:
   

   Phương trình $\sqrt{3}{\cot }^{2}x-4\cot x+\sqrt{3}=0$ có nghiệm là:

   A. $\left[\begin{array}{c}x=\frac{\pi }{3}+k\pi \\ x=\frac{\pi }{6}+k\pi \end{array}\right.\left(k\in Z\right)$

   Đáp án chính xác

   B. $\left[\begin{array}{c}x=\frac{\pi }{3}+k2\pi \\ x=\frac{\pi }{6}+k2\pi \end{array}\right.\left(k\in Z\right)$

   C. $\left[\begin{array}{c}x=-\frac{\pi }{3}+k\pi \\ x=-\frac{\pi }{6}+k\pi \end{array}\right.\left(k\in Z\right)$

   D. $\left[\begin{array}{c}x=-\frac{\pi }{3}+k2\pi \\ x=\frac{\pi }{6}+k\pi \end{array}\right.\left(k\in Z\right)$

   Trả lời:

   ĐK: $\sin x\ne 0\iff x\ne k\pi \left(k\in Z\right)$
   $\sqrt{3}{\cot }^{2}x-4\cot x+\sqrt{3}=0$
   Đặt cos x = t khi đó phương trình có dạng:
   $\sqrt{3}{t}^2-4t+\sqrt{3}=0$
   $\iff \left[\begin{array}{c}t=\frac{1}{\sqrt{3}}\\ t=\sqrt{3}\end{array}\right.$
   $\Rightarrow \left[\begin{array}{c}\cot x=\frac{1}{\sqrt{3}}\\ \cot x=\sqrt{3}\end{array}\right.$
   $\iff \left[\begin{array}{c}x=\frac{\pi }{3}+k\pi \\ x=\frac{\pi }{6}+k\pi \end{array}\right.\left(k\in Z\right)\left(tm\right)$
    
   Đáp án cần chọn là: A

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Nghiệm của phương trình 4sin22x+8cos2x−9=0 là:
   
   

   Câu hỏi:
   

   Nghiệm của phương trình $4{\sin }^{2}2x+8{\cos }^{2}x-9=0$ là:

   A. $x=\pm \frac{\pi }{6}+k\pi \left(k\in Z\right)$

   Đáp án chính xác

   B. $x=\pm \frac{\pi }{6}+k2\pi \left(k\in Z\right)$

   C. $x=\pm \frac{\pi }{3}+k\pi \left(k\in Z\right)$

   D. $\left[\begin{array}{c}x=\frac{\pi }{6}+k\pi \left(k\in Z\right)\\ x=\frac{\pi }{3}+k\pi \left(k\in Z\right)\end{array}\right.$

   Trả lời:

   Bước 1:
   $4{\sin }^{2}2x+8{\cos }^{2}x-9=0$
   $\iff 4\left(1-{\cos }^{2}2x\right)+8.\frac{1+\cos 2x}{2}-9=0$
   $\iff 4\left(1-{\cos }^{2}2x\right)+4.\left(1+\cos 2x\right)-9=0$
   $\iff 4\left(1-{\cos }^{2}2x\right)+4+4\cos 2x-9=0$
   $\iff 4-4{\cos }^{2}2x+4\cos 2x-5=0$
   $\iff -4{\cos }^{2}2x+4\cos 2x-1=0$
   Bước 2:
   Đặt $\cos 2x=t\left(-1\le t\le 1\right)$. Khi đó phương trình có dạng:
   $-4t^2+4t-1=0$
   $\iff -\left(4t^2-4t+1\right)=0$
   $\iff -{\left(2t-1\right)}^2=0$
   $\iff t=\frac{1}{2}\left(tm\right)$
   $\iff \cos 2x=\frac{1}{2}$
   $\iff \cos 2x=\cos \frac{\pi }{3}$
   $\iff 2x=\pm \frac{\pi }{3}+k2\pi$
   $\iff x=\pm \frac{\pi }{6}+k\pi \left(k\in Z\right)$
   Đáp án cần chọn là: A

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Số vị trí biểu diễn các nghiệm của phương trình 4sin2 x − 4sinx – 3 = 0  trên đường tròn lượng giác là:
   
   

   Câu hỏi:
   

   Số vị trí biểu diễn các nghiệm của phương trình 4sin² x − 4sinx – 3 = 0  trên đường tròn lượng giác là:

   A. 0     

   B. 1     

   C. 2      

   Đáp án chính xác

   D. 4

   Trả lời:

   4sin² x − 4sinx – 3 = 0  
   Đặt sinx = t (−1 ≤ t ≤ 1) khi đó phương trình có dạng:
   $4t^2-4t-3=0$
    
   $\iff \left[\begin{array}{c}t=\frac{3}{2}\left(ktm\right)\\ t=-\frac{1}{2}\left(tm\right)\end{array}\right.$

   $t=-\frac{1}{2}\iff \sin x=-\frac{1}{2}$
   $\iff \left[\begin{array}{c}x=-\frac{\pi }{6}+k2\pi \\ x=\frac{7\pi }{6}+k2\pi \end{array}\right.\left(k\in Z\right)$
   
    

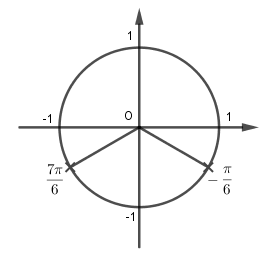
   Vây số vị trí biểu diễn các nghiệm của phương trình 4sin² x − 4sinx – 3 = 0 trên đường tròn lượng giác là 2 điểm như hình trên.
   Đáp án cần chọn là: C

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====