Câu hỏi:
Tìm các giá trị thực của tham số m để phương trình \(\left| {{x^2} – 3x + 2} \right| = m\;\) có bốn nghiệm thực phân biệt.
A.\(m \ge \frac{1}{4}\)
B. \(0 < m < \frac{1}{4}\)
Đáp án chính xác
C. \(m = 0\)
D. Không tồn tại
Trả lời:
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số
\(y = \left| {{x^2} – 3x + 2} \right|\)với đường thẳng y = m có tính chất song song với trục hoành.
Ta có \(y = \mid {x^2} – 3x + 2\mid = \left\{ {\begin{array}{*{20}{c}}{{x^2} – 3x + 2({x^2} – 3x + 2 \ge 0)}\\{ – {x^2} + 3x – 2({x^2} – 3x + 2 < 0)}\end{array}} \right.\)
Đồ thị hàm số \(y = \left| {{x^2} – 3x + 2} \right|\)được vẽ như sau:
+ Vẽ đồ thị hàm số \(y = {x^2} – 3x + 2\)+ Lấy đối xứng phần đồ thị phía dưới trục hoành qua trục hoành và xóa phần đồ thị dưới trục hoành đi.

Dựa trên đồ thị ta thấy phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi \(0 < m < \frac{1}{4}\)
Đáp án cần chọn là: B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho đồ thị hàm số \(y = a{x^2} + bx + c\) như hình vẽ.
Khẳng định nào sau đây là đúng: – ĐGNL-HN
Câu hỏi:
Cho đồ thị hàm số \(y = a{x^2} + bx + c\) như hình vẽ.
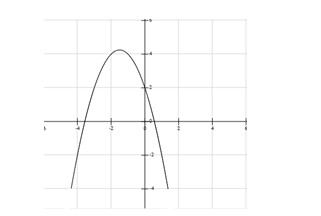
Khẳng định nào sau đây là đúng:A.a >0, b < 0, c >0
B. a < 0, b >0,c >0
C. a < 0, b < 0, c < 0
D. a < 0, b < 0, c >0
Đáp án chính xác
Trả lời:
Bề lõm của đồ thị quay xuống dưới nên hệ số a < 0.
Giao điểm của đồ thị hàm số với trục tung nằm trên trục có tung độ dương nên c >0
Hoành độ đỉnh \(x = – \frac{b}{{2a}} < 0\) Mà a < 0 nên b < 0.
Đáp án cần chọn là: D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Xác định Parabol (P):\(y = a{x^2} + bx + 2\;\) biết rằng Parabol đi qua hai điểm M(1;5) và N(2;−2). – ĐGNL-HN
Câu hỏi:
Xác định Parabol (P):\(y = a{x^2} + bx + 2\;\) biết rằng Parabol đi qua hai điểm M(1;5) và N(2;−2).
A.\(y = – 5{x^2} + 8x + 2\)
Đáp án chính xác
B. \(y = 10{x^2} + 13x + 2\)
C. \(y = – 10{x^2} – 13x + 2\)
D. \(y = 9{x^2} + 6x – 5\)
Trả lời:
Vì \(M,\,\,N \in (P)\) nên tọa độ của hai điểm M, N phải thỏa mãn phương trình của (P).
Do đó, ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{5 = a + b + 2}\\{ – 2 = 4a + 2b + 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = – 5}\\{b = 8}\end{array}} \right.\)
Vậy phương trình của (P)là:\(y = – 5{x^2} + 8x + 2\)
Đáp án cần chọn là: A====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Xác định Parabol (P):\(y = a{x^2} + bx – 5\) biết rằng Parabol đi qua điểm A(3;−4) và có trục đối xứng x = −\(\frac{3}{2}\). – ĐGNL-HN
Câu hỏi:
Xác định Parabol (P):\(y = a{x^2} + bx – 5\) biết rằng Parabol đi qua điểm A(3;−4) và có trục đối xứng x = −\(\frac{3}{2}\).
A.\(y = \frac{1}{{18}}{x^2} + \frac{1}{6}x – 5\)
Đáp án chính xác
B. \(y = \frac{1}{{18}}{x^2} + \frac{1}{6}x + 5\)
C. \(y = 3{x^2} + 9x – 9\)
D. \(y = – \frac{1}{{18}}{x^2} + \frac{1}{6}x – 5\)
Trả lời:
(P) đi qua điểm A(3;−4) nên \( – 4 = 9a + 3b – 5 \Leftrightarrow 9a + 3b = 1\).
Trục đối xứng \(x = – \frac{b}{{2a}} = – \frac{3}{2} \Leftrightarrow b = 3a\)
Suy ra hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{9a + 3b = 1}\\{3a – b = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{1}{{18}}}\\{b = \frac{1}{6}}\end{array}} \right.\)
Vậy phương trình của (P)là:\(y = \frac{1}{{18}}{x^2} + \frac{1}{6}x – 5\)
Đáp án cần chọn là: A====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Xác định Parabol (P):\(y = a{x^2} + bx + 3\;\) biết rằng Parabol có đỉnh I(3;−2). – ĐGNL-HN
Câu hỏi:
Xác định Parabol (P):\(y = a{x^2} + bx + 3\;\) biết rằng Parabol có đỉnh I(3;−2).
A.\(y = {x^2} – 6x + 3\)
B. \(y = – \frac{5}{9}{x^2} + \frac{{10}}{3}x + 3\)
C. \(y = 3{x^2} + 9x + 3\)
D. \(y = \frac{5}{9}{x^2} – \frac{{10}}{3}x + 3\)
Đáp án chính xác
Trả lời:
Ta có đỉnh của (P)có tọa độ
\(\left\{ {\begin{array}{*{20}{c}}{x = – \frac{b}{{2a}} = 3}\\{y = 9a + 3b + 3 = – 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{6a + b = 0}\\{9a + 3b = – 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{5}{9}}\\{b = – \frac{{10}}{3}}\end{array}} \right.\)
Suy ra phương trình của Parabol (P)là:\(y = \frac{5}{9}{x^2} – \frac{{10}}{3}x + 3\)
Đáp án cần chọn là: D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Viết phương trình của Parabol (P) biết rằng (P) đi qua các điểm A(0;2),B(−2;5),C(3;8) – ĐGNL-HN
Câu hỏi:
Viết phương trình của Parabol (P) biết rằng (P) đi qua các điểm A(0;2),B(−2;5),C(3;8)
A.\(\)\(y = \frac{7}{{10}}{x^2} + \frac{1}{{10}}x – 2\)
B. \(y = \frac{7}{{10}}{x^2} – \frac{1}{{10}}x + 2\)
Đáp án chính xác
C. \(y = \frac{7}{{10}}{x^2} – \frac{1}{{10}}x – 2\)
D. \(y = \frac{7}{{10}}{x^2} + \frac{1}{{10}}x + 2\)
Trả lời:
Phương trình (P) có dạng \(y = a{x^2} + bx + c\,\,\,\,\left( {a \ne 0} \right)\)
Ba điểm A,B,C thuộc (P) nên tọa độ của chúng phải thỏa mãn phương trình (P)
Do đó, ta có hệ phương trình\(\left\{ {\begin{array}{*{20}{c}}{2 = a{{.0}^2} + b.0 + c}\\{5 = a.{{( – 2)}^2} + b.( – 2) + c}\\{8 = a{{.3}^2} + b.3 + c}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = \frac{7}{{10}}}\\{b = – \frac{1}{{10}}}\\{c = 2}\end{array}} \right.\)
Suy ra phương trình của (P) là: \(y = \frac{7}{{10}}{x^2} – \frac{1}{{10}}x + 2\)Đáp án cần chọn là: B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
