Câu hỏi:
Một viên gạch hình vuông có cạnh thay đổi được đặt nội tiếp trong một hình vuông có cạnh bằng 20cm, tạo thành bốn tam giác xung quanh như hình vẽ.
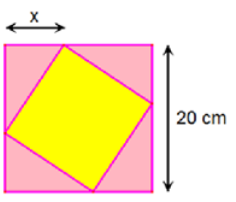
Tìm tập hợp các giá trị của x để diện tích viên gạch không vượt quá 208cm2.
A.\(8 \le x \le 12\)
Đáp án chính xác
B. \(6 \le x \le 14\)
C. \(12 \le x \le 14\)
D. \(12 \le x \le 18\)
Trả lời:
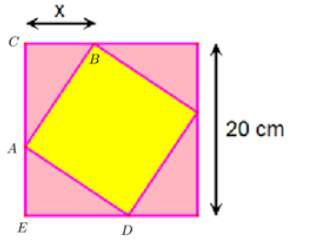
Ta có:\(\angle CAB + \angle BAD + \angle DAE = {180^o}\)
\( \Rightarrow \angle CAB + \angle EAD = {90^o}\)
Mà \(\angle CAB + \angle CBA = {90^o}\) (\(\Delta CAB\)vuông tại C)
\( \Rightarrow \angle CBA = \angle EAD\) kết hợp\(AB = AD\,\,\,\left( {gt} \right)\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {\rm{\Delta }}CAB = {\rm{\Delta }}EDA\,\,\,\left( {ch – gn} \right)}\\{ \Rightarrow CB = EA = x \Rightarrow CA = CE – EA = 20 – x\,\,\,\,\left( {cm} \right)}\end{array}\)
Diện tích viên gạch là\(S = A{B^2} = C{B^2} + C{A^2} = {x^2} + {\left( {20 – x} \right)^2}\)
Vì \(S \le 208 \Leftrightarrow {x^2} + {\left( {20 – x} \right)^2} \le 208 \Leftrightarrow 2{x^2} – 40x + 192 \le 0 \Leftrightarrow 8 \le x \le 12\)
Đáp án cần chọn là: A
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập nghiệm SS của bất phương trình \(5x – 1 \ge \frac{{2x}}{5} + 3\)là: – ĐGNL-HN
Câu hỏi:
Tập nghiệm SS của bất phương trình \(5x – 1 \ge \frac{{2x}}{5} + 3\)là:
A.\(S = \mathbb{R}.\)
B. \(S = \left( { – \infty ;2} \right).\)
C. \(S = \left( { – \frac{5}{2}; + \infty } \right).\)
D. \(S = \left[ {\frac{{20}}{{23}}; + \infty } \right).\)
Đáp án chính xác
Trả lời:
Bất phương trình\(5x – 1 \ge \frac{{2x}}{5} + 3\)
\( \Leftrightarrow 25x – 5 \ge 2x + 15 \Leftrightarrow 23x \ge 20 \Leftrightarrow x \ge \frac{{20}}{{23}}.\)
Đáp án cần chọn là: D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tổng các nghiệm nguyên của bất phương trình \(\frac{{x – 2}}{{\sqrt {x – 4} }} \le \frac{4}{{\sqrt {x – 4} }}\) bằng: – ĐGNL-HN
Câu hỏi:
Tổng các nghiệm nguyên của bất phương trình \(\frac{{x – 2}}{{\sqrt {x – 4} }} \le \frac{4}{{\sqrt {x – 4} }}\) bằng:
A.15.
B.11.
Đáp án chính xác
C.26.
D.0.
Trả lời:
Điều kiện: x >4.
Bất phương trình tương đương :
\(x – 2 \le 4 \Leftrightarrow x \le 6 \Rightarrow 4 < x \le 6\)
Mà \(x \in \mathbb{Z} \Rightarrow x = 5;x = 6 \Rightarrow S = 5 + 6 = 11\)
Đáp án cần chọn là: B
</>====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tổng các nghiệm nguyên của bất phương trình \(x\left( {2 – x} \right) \ge x\left( {7 – x} \right) – 6\left( {x – 1} \right)\) trên đoạn \(\left[ { – 10;10} \right]\;\)bằng: – ĐGNL-HN
Câu hỏi:
Tổng các nghiệm nguyên của bất phương trình \(x\left( {2 – x} \right) \ge x\left( {7 – x} \right) – 6\left( {x – 1} \right)\) trên đoạn \(\left[ { – 10;10} \right]\;\)bằng:
A.5.
B.6.
C.21.
D.40.
Đáp án chính xác
Trả lời:
Bất phương trình \(x\left( {2 – x} \right) \ge x\left( {7 – x} \right) – 6\left( {x – 1} \right)\)
\( \Leftrightarrow 2x – {x^2} \ge 7x – {x^2} – 6x + 6 \Leftrightarrow x \ge 6\)Mà\(x \in \mathbb{Z};x \in \left[ { – 10;10} \right] \Rightarrow x \in \left\{ {6;7;8;9;10} \right\}\)
Vậy tổng các nghiệm nguyên cần tìm là: 6+7+8+9+10=40.
Đáp án cần chọn là: D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập nghiệm của bất phương trình: \( – {x^2} + 6x + 7\; \ge 0\;\) là: – ĐGNL-HN
Câu hỏi:
Tập nghiệm của bất phương trình: \( – {x^2} + 6x + 7\; \ge 0\;\) là:
A.\(\left( { – \infty ; – 1} \right] \cup \left[ {7; + \infty } \right)\)
B. \(\left[ { – 1;7} \right]\)
Đáp án chính xác
C. \(\left( { – \infty ; – 7} \right] \cup \left[ {1; + \infty } \right)\)
D. \(\left[ { – 7;1} \right]\)Trả lời:
Trả lời:
Ta có \( – {x^2} + 6x + 7 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 7}\\{x = – 1}\end{array}} \right.\)
Bảng xét dấu
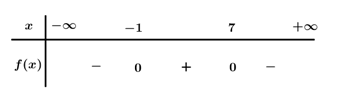
Dựa vào bảng xét dấu \( – {x^2} + 6x + 7\; \ge 0 \Leftrightarrow – 1 \le x \le 7.\)Đáp án cần chọn là: B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Giải bất phương trình \( – 2{x^2} + 3x – 7 \ge 0.\). – ĐGNL-HN
Câu hỏi:
Giải bất phương trình \( – 2{x^2} + 3x – 7 \ge 0.\).
A.S=0.
B.\(S = \left\{ 0 \right\}.\)
C. \(S = \emptyset .\)
Đáp án chính xác
D. \(S = \mathbb{R}.\)
Trả lời:
Ta có\( – 2{x^2} + 3x – 7\; = 0\) vô nghiệm.
Bảng xét dấu
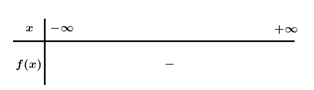
Dựa vào bảng xét dấu\( – 2{x^2} + 3x – 7 \ge 0\, \Leftrightarrow \,x \in \emptyset \)Đáp án cần chọn là: C
====== **** mời các bạn xem câu tiếp bên dưới **** =====
