Câu hỏi:
Cho tứ diện đều SABC. Gọi I là trung điểm của AB,M là một điểm di động trên đoạn AI. Gọi (P) là mặt phẳng qua M và song song với SI,IC, biết AM=x. Thiết diện tạo bởi mp(P) và tứ diện SABC có chu vi là:
A.\(3x\left( {1 + \sqrt 3 } \right)\)
B. \(2x\left( {1 + \sqrt 3 } \right)\)
Đáp án chính xác
C. \(x\left( {1 + \sqrt 3 } \right)\)
D. Không xác định
Trả lời:
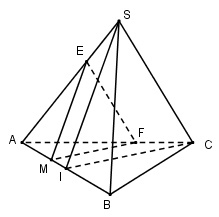Trong mp(ABC) kẻ\(MF//IC\left( {F \in AC} \right)\) trong mp(SAB) kẻ \(ME//SI\left( {E \in SA} \right)\)Do đó mp(P) chính là (MEF) và thiết diện tạo bởi mp(P) và tứ diện đều SABC là tam giác MEF.Gọi aa là cạnh của tứ diện đều SABC.Xét tam giác đều ABC và tam giác SAB là những tam giác đều cạnh a nên\(CI = SI = \frac{{a\sqrt 3 }}{2}\)Trong (ABC) ta có:\(\frac{{AM}}{{AI}} = \frac{{ME}}{{SI}} \Leftrightarrow \frac{x}{{\frac{a}{2}}} = \frac{{ME}}{{\frac{{a\sqrt 3 }}{2}}} \Leftrightarrow ME = x\sqrt 3 .\)Trong (SAB) ta có: \(\frac{{AM}}{{AI}} = \frac{{MF}}{{CI}} \Leftrightarrow \frac{x}{{\frac{a}{2}}} = \frac{{MF}}{{\frac{{a\sqrt 3 }}{2}}} \Leftrightarrow MF = x\sqrt 3 .\)Ta lại có:\(\frac{{AM}}{{AI}} = \frac{{AF}}{{AC}} = \frac{{AE}}{{AS}} \Rightarrow EF//SC\) (Định lí Ta-let đảo)\( \Rightarrow \frac{{EF}}{{SC}} = \frac{{AF}}{{AC}} = \frac{{AM}}{{AI}} \Leftrightarrow \frac{{EF}}{a} = \frac{x}{{\frac{a}{2}}} \Leftrightarrow EF = 2x\)Vậy chu vi tam giác MEF bằng \(ME + MF + EF = x\sqrt 3 + x\sqrt 3 + 2x = 2x\left( {1 + \sqrt 3 } \right)\)Đáp án cần chọn là: B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số điểm chung của đường thẳng và mặt phẳng không thể là: – ĐGNL-HN
Câu hỏi:
Số điểm chung của đường thẳng và mặt phẳng không thể là:
A.chỉ hai điểm
Đáp án chính xác
B.một điểm
C.không có điểm nào
D.vô số điểm
Trả lời:
Đường thẳng và mặt phẳng nếu có hai điểm chung thì sẽ có vô số điểm chung nên không thể chỉ có hai điểm chung.Đáp án cần chọn là: A
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Nếu đường thẳng d và mặt phẳng (α) không có điểm chung thì chúng – ĐGNL-HN
Câu hỏi:
Nếu đường thẳng d và mặt phẳng (α) không có điểm chung thì chúng
A.song song
Đáp án chính xác
B.cắt nhau
C.chéo nhau
D.trùng nhau
Trả lời:
Nếu đường thẳng d và mặt phẳng (α) không có điểm chung thì chúng song song.Đáp án cần chọn là: A
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho đường thẳng d và mặt phẳng (α) như hình vẽ, số điểm chung của d và (α) là: – ĐGNL-HN
Câu hỏi:
Cho đường thẳng d và mặt phẳng (α) như hình vẽ, số điểm chung của d và (α) là:
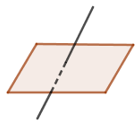
A.0
B.1
Đáp án chính xác
C.2
D.vô số
Trả lời:
Từ hình vẽ ta thấy d cắt (α) tại duy nhất một điểm.Đáp án cần chọn là: B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tứ diện ABCD. Chọn kết luận đúng: – ĐGNL-HN
Câu hỏi:
Cho tứ diện ABCD. Chọn kết luận đúng:
A.\(AD \subset \left( {ABC} \right)\)
b.\(AD \cap \left( {ABC} \right) = C\)
c.\(AB \subset \left( {ABC} \right)\)
Đáp án chính xác
d.\(AC//\left( {ABD} \right)\)
Trả lời:
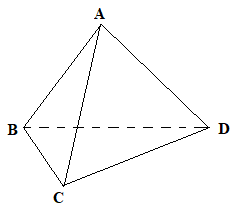
Từ hình vẽ ta thấy:
+) Đường thẳng AD cắt mặt phẳng (ABC) tại điểm duy nhất A nên đáp án A, B đều sai.
\( + )A \in \left( {ABC} \right),B \in \left( {ABC} \right) \Rightarrow AB \subset \left( {ABC} \right)\) nên C đúng.
+) Đường thẳng AC cắt mặt phẳng (ABD) tại điểm duy nhất A nên D sai.Đáp án cần chọn là: C
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Nếu một đường thẳng d không nằm trong mặt phẳng (α) mà nó song song với đường thẳng d′ trong (α) thì: – ĐGNL-HN
Câu hỏi:
Nếu một đường thẳng d không nằm trong mặt phẳng (α) mà nó song song với đường thẳng d′ trong (α) thì:
A.\(d//(\alpha )\;\)
Đáp án chính xác
B.d cắt \(\left( \alpha \right)\;\)
C. \(d \subset \left( \alpha \right)\)
D. \(d \supset \left( \alpha \right)\)
Trả lời:
Nếu đường thẳng d không nằm trong mặt phẳng (α) mà d song song với một đường thẳng d′ nằm trong (α) thì d song song với (α).
Đáp án cần chọn là: A====== **** mời các bạn xem câu tiếp bên dưới **** =====
