Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M,N,P,Q, lần lượt là các điểm nằm trên các cạnh BC,SC,SD,AD sao cho MN//BS,NP//CD,MQ//CD. Hỏi PQ song song với mặt phẳng nào sau đây?
A.mp(SBC)
B.mp(SAB)
Đáp án chính xác
C.mp(SAD)
D.mp(SCD)
Trả lời:
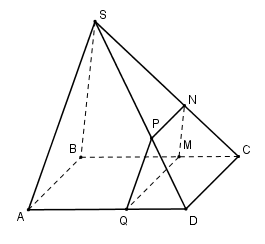Vì\(MN//BS\) nên \(\frac{{CN}}{{CS}} = \frac{{CM}}{{CB}}\) (Định lí Ta – let) (1)Vì \(MQ//CD//AB\) nên\(\frac{{CM}}{{CB}} = \frac{{DQ}}{{DA}}\) (2)Vì \(NP//CD\) nên \(\frac{{CN}}{{CS}} = \frac{{DP}}{{DS}}\) (Định lí Ta – let) (3)Từ (1), (2) và (3) suy ra\(\frac{{DP}}{{DS}} = \frac{{DQ}}{{DA}} \Rightarrow PQ//SA\) (Định lí Ta – let đảo)Ta có: \(SA \subset \left( {SAB} \right)\,\,;\,\,SA \subset \left( {SAD} \right)\)Tuy nhiên\(PQ \subset \left( {SAD} \right)\) nên PQ không song song với mp(SAD).Ngoài ra PQ không nằm trong (SAB) nên PQ//(SAB)Vậy PQ//(SAB).Đáp án cần chọn là: B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Số điểm chung của đường thẳng và mặt phẳng không thể là: – ĐGNL-HN
Câu hỏi:
Số điểm chung của đường thẳng và mặt phẳng không thể là:
A.chỉ hai điểm
Đáp án chính xác
B.một điểm
C.không có điểm nào
D.vô số điểm
Trả lời:
Đường thẳng và mặt phẳng nếu có hai điểm chung thì sẽ có vô số điểm chung nên không thể chỉ có hai điểm chung.Đáp án cần chọn là: A
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Nếu đường thẳng d và mặt phẳng (α) không có điểm chung thì chúng – ĐGNL-HN
Câu hỏi:
Nếu đường thẳng d và mặt phẳng (α) không có điểm chung thì chúng
A.song song
Đáp án chính xác
B.cắt nhau
C.chéo nhau
D.trùng nhau
Trả lời:
Nếu đường thẳng d và mặt phẳng (α) không có điểm chung thì chúng song song.Đáp án cần chọn là: A
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho đường thẳng d và mặt phẳng (α) như hình vẽ, số điểm chung của d và (α) là: – ĐGNL-HN
Câu hỏi:
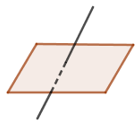
Cho đường thẳng d và mặt phẳng (α) như hình vẽ, số điểm chung của d và (α) là:
A.0
B.1
Đáp án chính xác
C.2
D.vô số
Trả lời:
Từ hình vẽ ta thấy d cắt (α) tại duy nhất một điểm.Đáp án cần chọn là: B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tứ diện ABCD. Chọn kết luận đúng: – ĐGNL-HN
Câu hỏi:
Cho tứ diện ABCD. Chọn kết luận đúng:
A.\(AD \subset \left( {ABC} \right)\)
b.\(AD \cap \left( {ABC} \right) = C\)
c.\(AB \subset \left( {ABC} \right)\)
Đáp án chính xác
d.\(AC//\left( {ABD} \right)\)
Trả lời:
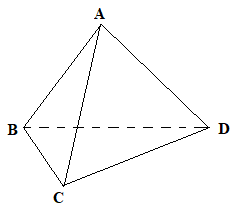
Từ hình vẽ ta thấy:
+) Đường thẳng AD cắt mặt phẳng (ABC) tại điểm duy nhất A nên đáp án A, B đều sai.
\( + )A \in \left( {ABC} \right),B \in \left( {ABC} \right) \Rightarrow AB \subset \left( {ABC} \right)\) nên C đúng.
+) Đường thẳng AC cắt mặt phẳng (ABD) tại điểm duy nhất A nên D sai.Đáp án cần chọn là: C
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Nếu một đường thẳng d không nằm trong mặt phẳng (α) mà nó song song với đường thẳng d′ trong (α) thì: – ĐGNL-HN
Câu hỏi:
Nếu một đường thẳng d không nằm trong mặt phẳng (α) mà nó song song với đường thẳng d′ trong (α) thì:
A.\(d//(\alpha )\;\)
Đáp án chính xác
B.d cắt \(\left( \alpha \right)\;\)
C. \(d \subset \left( \alpha \right)\)
D. \(d \supset \left( \alpha \right)\)
Trả lời:
Nếu đường thẳng d không nằm trong mặt phẳng (α) mà d song song với một đường thẳng d′ nằm trong (α) thì d song song với (α).
Đáp án cần chọn là: A====== **** mời các bạn xem câu tiếp bên dưới **** =====
