Giải bài tập Toán 12 Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn
1. Tốc độ thay đổi của một đại lượng
Luyện tập 1 trang 33 Toán 12 Tập 1: Khi máu di chuyển từ tim qua các động mạch chính rồi đến các mao mạch và quay trở lại qua các tĩnh mạch, huyết áp tâm thu (tức là áp lực của máu lên động mạch khi tim co bóp) liên tục giảm xuống. Giả sử một người có huyết áp tâm thu P (tính bằng mmHg) được cho bởi hàm số , trong đó thời gian t được tính bằng giây. Tính tốc độ thay đổi của huyết áp sau 5 giây kể từ khi máu rời tim.
Lời giải:
Hàm số thể hiện tốc độ thay đổi của huyết áp là:
Tốc độ thay đổi của huyết áp sau 5 giây kể từ khi máu rời tim là:
Tốc độ thay đổi huyết áp sau 5 giây kể từ khi máu rời tim là giảm
2. Một vài bài toán tối ưu hóa đơn giản
Luyện tập 2 trang 38 Toán 12 Tập 1: Anh An chèo thuyền từ điểm A trên bờ một con sông thẳng rộng 3km và muốn đến điểm B ở bờ đối diện cách 8km về phía hạ lưu càng nhanh càng tốt (H.1.35). Anh An có thể chèo thuyền trực tiếp qua sông đến điểm C rồi chạy bộ đến B, hoặc anh có thể chèo thuyển thẳng đến B, hoặc anh cũng có thể chèo thuyền đến một điểm D nào đó giữa C và B rồi chạy bộ đến B. Nếu vận tốc chèo thuyền là 6km/h và vận tốc chạy bộ là 8km/h thì anh An phải chèo thuyền sang bờ ở điểm nào để đến B càng sớm càng tốt? (Giả sử rằng vận tốc của nước là không đáng kể so với vận tốc chèo thuyền của anh An).
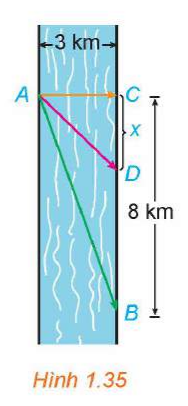
Lời giải:
Gọi độ dài đoạn CD là x (km )
Quãng đường AD dài:
Quãng đường BD dài
Thời gian người đó đi đến B bằng cách chèo thuyền đến một điểm D nào đó giữa C và B rồi chạy bộ đến B là: (giờ)
Xét hàm số với
Ta có:
Bảng biến thiên:
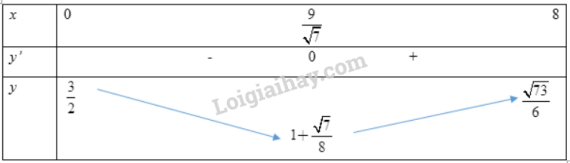
Vậy anh An phải chèo thuyền sang bờ ở điểm D cách B một khoảng bằng thì đến B sớm nhất.
Vận dụng trang 40 Toán 12 Tập 1: Một nhà sản xuất trung bình bán được 1 000 ti vi màn hình phẳng mỗi tuần với giá 14 triệu đồng một chiếc. Một cuộc khảo sát thị trường chỉ ra rằng nếu cứ giảm giá bán 500 nghìn đồng, số lượng ti vi bán ra sẽ tăng thêm khoảng 100 ti vi mỗi tuần.
a) Tìm hàm cầu.
b) Công ty nên giảm giá bao nhiêu cho người mua để doanh thu là lớn nhất?
c) Nếu hàm chi phí hằng tuần là (triệu đồng), trong đó x là số ti vi bán ra trong tuần, nhà sản xuất nên đặt giá bán như thế nào để lợi nhuận là lớn nhất?
Lời giải:
a) Gọi p (triệu đồng) là giá của mỗi ti vi, x là số ti vi. Khi đó, hàm cầu là .
Theo giả thiết, tốc độ thay đổi của x tỉ lệ với tốc độ thay đổi của p nên hàm số là hàm số bậc nhất nên. Do đó, (a khác 0).
Giá tiền ứng với , giá tiền ứng với
Do đó, phương trình đường thẳng đi qua hai điểm (1000; 14) và (1 100; 13,5). Ta có hệ phương trình: (thỏa mãn)
Vậy hàm cầu là:
b) Vì
Hàm doanh thu từ tiền bán ti vi là:
Để doanh thu là lớn nhất thì ta cần tìm p sao cho R đạt giá trị lớn nhất.
Ta có:
Bảng biến thiên:
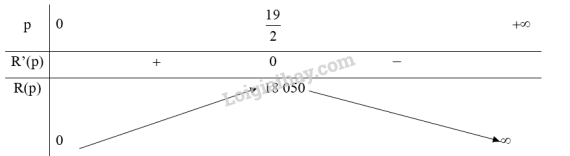
Vậy công ty nên giảm giá số tiền một chiếc ti vi là: (triệu đồng) thì doanh thu là lớn nhất.
c) Doanh thu bán hàng của x sản phẩm là: (triệu đồng)
Do đó, hàm số thể hiện lợi nhuận thu được khi bán x sản phẩm là:
(triệu đồng).
Để lợi nhuận là lớn nhất thì P(x) là lớn nhất.
Ta có:
Bảng biến thiên:
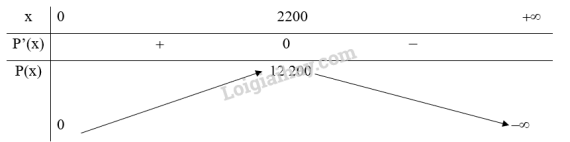
Vậy có 2200 ti vi được bán ra thì lợi nhuận là cao nhất. Số ti vi mua tăng lên là: (chiếc)
Vậy cửa hàng nên đặt giá bán là: (triệu đồng)
Bài tập
Bài 1.26 trang 40 Toán 12 Tập 1: Giả sử một hạt chuyển động trên một trục thẳng đứng chiều dương hướng lên trên sao cho tọa độ của hạt (đơn vị: mét) tại thời điểm t (giây) là .
a) Tìm các hàm vận tốc và gia tốc.
b) Khi nào thì hạt chuyển động lên trên và khi nào thì hạt chuyển động xuống dưới?
c) Tìm quãng đường hạt đi được trong khoảng thời gian .
d) Khi nào hạt tăng tốc? Khi nào hạt giảm tốc?
Lời giải:
a) Hàm vận tốc là: ,
Hàm gia tốc là: ,
b) Hạt chuyển động lên trên khi (do )
Hạt chuyển động xuống dưới khi (do )
c) Ta có:
Vậy quãng đường vật đi được trong thời gian là 9m.
d) Hạt tăng tốc khi tăng hay Do đó,
Hạt giảm tốc khi giảm hay (không thỏa mãn do )
Bài 1.27 trang 41 Toán 12 Tập 1: Giả sử chi phí (tính bằng trăm nghìn đồng) để sản xuất x đơn vị hàng hóa nào đó là:
a) Tìm hàm chi phí biên.
b) Tìm C’(100) và giải thích ý nghĩa của nó.
c) So sánh C’(100) với chi phí sản xuất đơn vị hàng hóa thứ 101.
Lời giải:
a) Hàm chi phí biên là: .
b) Ta có: (trăm nghìn đồng)
Chi phí biên tại là 250 000 đồng, nghĩa là chi phí để sản xuất thêm một đơn vị hàng hóa tiếp theo (đơn thứ 101) là khoảng 250 000 đồng.
c) Chi phí sản xuất đơn hàng thứ 101 là:
(trăm nghìn đồng)
Giá trị này xấp xỉ với chi phí biên C’(100) đã tính ở câu b.
Bài 1.28 trang 41 Toán 12 Tập 1: Người quản lí của một khu chung cư có 100 căn hộ cho thuê nhận thấy rằng tất cả các căn hộ sẽ có người thuê nếu giá thuê một căn hộ là 8 triệu đồng một tháng. Một cuộc khảo sát thị trường cho thấy rằng, trung bình cứ mỗi lần tăng giá thuê căn hộ thêm 100 nghìn đồng thì sẽ có thêm một căn hộ bị bỏ trống. Người quản lí nên đặt giá thuê mỗi căn hộ là bao nhiêu để doanh thu là lớn nhất?
Lời giải:
Gọi x là số lần tăng giá 100 nghìn đồng ().
Khi đó, số căn được cho thuê là: (căn)
Tổng số tiền thu được trong một tháng là:
với mọi .
Dấu “=” xảy ra khi (thỏa mãn)
Vậy để thu được doanh thu là lớn nhất thì người quản lí nên đặt giá thuê mỗi căn hộ là: (đồng).
Bài 1.29 trang 41 Toán 12 Tập 1: Giả sử hàm cầu đối với một loại hàng hóa được cho bởi công thức , trong đó p là giá bán (nghìn đồng) của mỗi đơn vị sản phẩm và x là số lượng đơn vị sản phẩm đã bán.
a) Tìm công thức tính x như là hàm số của p. Tìm tập xác định của hàm số này. Tính số đơn vị sản phẩm đã bán khi giá bán của mỗi đơn vị sản phẩm là 240 nghìn đồng.
b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số . Từ đồ thị đã vẽ, hãy cho biết:
– Số lượng đơn vị sản phẩm bán được sẽ thay đổi thế nào khi giá bán p tăng;
– Ý nghĩa thực tiễn của giới hạn .
Lời giải:
a) Tìm công thức tính x như là hàm số của p. Tìm tập xác định của hàm số này. Tính số đơn vị sản phẩm đã bán khi giá bán của mỗi đơn vị sản phẩm là 240 nghìn đồng.
Vì
Tập xác định của hàm số là:
Với ta có:
Vậy với giá bán mỗi đơn vị sản phẩm là 240 nghìn đồng thì bán được 47,5 đơn vị sản phẩm.
b) Khảo sát sự biến thiên của hàm số:
1. Tập xác định của hàm số:
2. Sự biến thiên:
Ta có: với mọi .
Hàm số nghịch biến trên khoảng .
Hàm số không có cực trị.
Giới hạn:
Do đó, đồ thị hàm số với nhận đường thẳng làm tiệm cận đứng.
Bảng biến thiên:

3. Đồ thị:
Ta có:
Đồ thị hàm số cắt trục hoành tại điểm (354; 0).
Đồ thị hàm số đi qua các điểm (300; 18); (200; 77).
Đồ thị hàm số với là đường màu xanh:
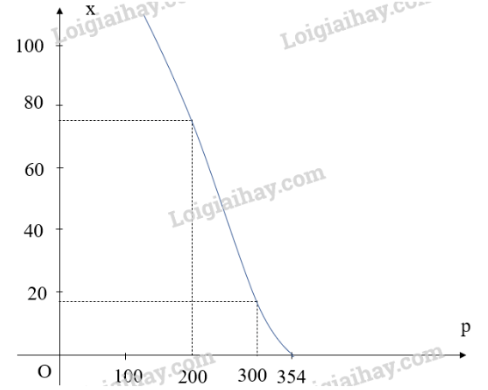
– Số lượng đơn vị sản phẩm bán sẽ giảm đi khi giá bán tăng, và sẽ không bán được sản phẩm nào nếu giá bán là 354 nghìn đồng
– Ý nghĩa thực tiễn của giới hạn : Vì nên giá bán càng thấp thì số lượng đơn vị sản phẩm sẽ bán được càng nhiều.
Xem thêm các bài giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:
Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Bài 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn
Bài tập cuối chương 1
Bài 6. Vectơ trong không gian
Bài 7. Hệ trục toạ độ trong không gian
Bài 8. Biểu thức toạ độ của các phép toán vectơ
Lý thuyết Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn
1. Tốc độ thay đổi của một đại lượng
– Nếu s = s(t) là hàm vị trí của một vật chuyển đọng trên một đường thẳng thì v = s’(t) biểu thị vận tốc tức thời của vật. Tốc độ thay đổi tức thời của vận tốc theo thời gian là gia tốc tức thời của vật: a(t) = v’(t) = s’’(t) – Nếu C = C(t) là nồng độ của một chất tham gia phản ứng hóa học tại thời điểm t, thì C’(t) là tốc độ phản ứng tức thời của chất đó tại thời điểm t – Nếu P = P(t) là số lượng cá thể trong một quần thể động vật hoặc thực vật tại thời điểm t, thì P’(t) biểu thị tốc độ tăng trưởng tức thời của quần thể tại thời điểm t – Nếu C = C(x) là hàm chi phí, tức là tổng chi phí khi sản xuất x đơn vị hàng hóa, thì tốc độ thay đổi tức thời C’(x) của chi phí đó đối với số lượng đơn vị hàng được sản xuất được gọi là chi phí biên – Về ý nghĩa kinh tế, chi phí biên C’(x) xấp xỉ với chi phí để sản xuất thêm một đơn vị hàng hóa tiếp theo, tức là đơn vị hàng hóa thứ x + 1 |
Ví dụ: Khi bỏ qua sức cản của không khí, độ cao (mét) của một vật được phóng thẳng đứng lên trên từ điểm cách mặt đất 2m với vận tốc ban đầu 24,5 m/s là
a) Tìm vận tốc của vật sau 2s
b) Khi nào vật đạt độ cao lớn nhất và độ cao lớn nhất đó là bao nhiêu?
c) Khi nào thì vật chạm đất và vận tốc của vật lúc chạm đất là bao nhiêu?
Lời giải
a) Ta có: v = h’(t) = 24,5 – 9,8t (m/s)
Do đó v(2) = 24,5 – 9,8.2 = 4,9 (m/s)
b) Vì h(t) là hàm số bậc hai có hệ số a = -4,9 < 0 nên h(t) đạt giá trị lớn nhất tại . Khi đó, độ cao lớn nhất của vật là h(2,5) = 32,625 (m)
c) Vật chạm đất khi h = 0, tức là hay
Vận tốc của vật lúc chạm đất là v(5,08) = 24,5 – 9,8.5,08 = -25,284 (m/s)
Vận tốc âm chứng tỏ chiều chuyện động của vật là ngược chiều dương (hướng lên trên) của trục đã chọn
2. Một vài bài toán tối ưu hóa đơn giản
Quy trình giải một bài toán tối ưu hóa
Bước 1. Xác định đại lượng Q mà ta cần làm cho giá trị của đại lượng ấy lớn nhất hoặc nhỏ nhất và biểu diễn nó qua các đại lượng trong bài toán Bước 2. Chọn một đại lượng thích hợp nào đó, kí hiệu là x, và biểu diễn các đại lượng khác ở Bước 1 theo x. Khi đó, đại lượng Q sẽ là hàm số của một biến x. Tìm tập xác định của hàm số Q = Q(x) Bước 3. Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số Q = Q(x) bằng các phương pháp đã biết và kết luận |
Ví dụ: Một nhà sản xuất cần làm những hộp đựng hình trụ có thể tích 1 lít. Tìm các kích thước của hộp đựng để chi phí vật liệu dùng để sản xuất là nhỏ nhất
Đổi 1 lít = 1000 cm3
Gọi r (cm) là bán kính đáy của hình trụ, h (cm) là chiều cao của hình trụ
Diện tích toàn phần của hình trụ là
Do thể tích của hình trụ là 1000 cm3 nên ta có: hay
Do đó, diện tích toàn phần của hình trụ là
Ta cần tìm r sao cho S đạt giá trị nhỏ nhất. Ta có:
BBT
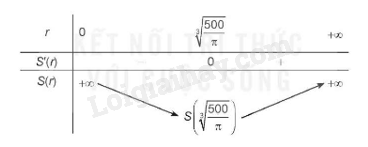
Khi đó:
Vậy cần sản xuất các hộp đựng hình trụ có bán kính đáy và chiều cao