Sách bài tập Toán 12 Bài 3 (Kết nối tri thức): Đường tiệm cận của đồ thị hàm số

Giải SBT Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số

Bài 1.21 trang 19 SBT Toán 12 Tập 1: Cho hàm số $y=f\left(x\right)=\frac{x^2+3x-10}{x-2}$ . Đồ thị hàm số f(x) có tiệm cận đứng không?

Lời giải:

Ta có: $\underset{x\to 2}{\lim }f\left(x\right)=\underset{x\to 2}{\lim }\frac{\left(x-2\right)\left(x+5\right)}{x-2}$= $\underset{x\to 2}{\lim }$(x + 5) = 7.

Hơn nữa y = f(x) liên tục tại mọi điểm x ≠ 2. Do đó, đồ thị hàm f(x) không có tiệm cận đứng.

Bài 1.22 trang 19 SBT Toán 12 Tập 1: Tìm các đường tiệm cận của đồ thị các hàm số sau:

a) y = $\frac{x+1}{2x-3};$

b) y = $\frac{3x-1}{x+2}.$

Lời giải:

a) Ta có: $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{x+1}{2x-3}=\frac{1}{2}$ ;

               $\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{x+1}{2x-3}=\frac{1}{2}$ .

Do đó, đường thẳng y = $\frac{1}{2}$  là tiệm cận ngang của đồ thị hàm số.

              $\underset{x\to {\frac{3}{2}}^{+}}{\lim }y=\underset{x\to {\frac{3}{2}}^{+}}{\lim }\frac{x+1}{2x-3}=+\infty$ ;

              $\underset{x\to {\frac{3}{2}}^{-}}{\lim }y=\underset{x\to {\frac{3}{2}}^{-}}{\lim }\frac{x+1}{2x-3}=-\infty$ .

Do đó, đường thẳng x = $\frac{3}{2}$  là đường tiệm cận đứng của đồ thị hàm số.

b) Ta có: $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{3x-1}{x+2}=3$ ;

               $\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{3x-1}{x+2}=3$ .

Do đó, đường thẳng y = 3 là tiệm cận ngang của đồ thị hàm số.

              $\underset{x\to -2^{+}}{\lim }y=\underset{x\to -2^{+}}{\lim }\frac{3x-1}{x+2}=-\infty$ ;

              $\underset{x\to -2^{-}}{\lim }y=\underset{x\to -2^{-}}{\lim }\frac{3x-1}{x+2}=+\infty$ .

Do đó, đường thẳng x = −2 là đường tiệm cận đứng của đồ thị hàm số.

Bài 1.23 trang 19 SBT Toán 12 Tập 1: Tìm tiệm cận đứng và tiệm cận xiên của đồ thị hàm số sau:

a) $y=\frac{x^2-x-5}{x-2};$

b) y = $\frac{3x^2+8x-2}{x+3}.$

Lời giải:

a) $y=\frac{x^2-x-5}{x-2};$

Ta có: $\underset{x\to 2^{+}}{\lim }y=\underset{x\to 2^{+}}{\lim }\frac{x^2-x-5}{x-2}=-\infty$ ;

           $\underset{x\to 2^{-}}{\lim }y=\underset{x\to 2^{-}}{\lim }\frac{x^2-x-5}{x-2}=+\infty$ .

Do đó, đường thẳng x = 2 là đường tiệm cận đứng của đồ thị hàm số.

            $\underset{x\to +\infty }{\lim }\frac{y}{x}=\underset{x\to +\infty }{\lim }\frac{x^2-x-5}{\left(x-2\right)x}=1$ .

            $\underset{x\to +\infty }{\lim }\left(y-x\right)=\underset{x\to +\infty }{\lim }\left[\frac{x^2-x-5}{x-2}-x\right]=\underset{x\to +\infty }{\lim }\frac{x-5}{x-2}=1$ .

Do đó đường thẳng y = x + 1 là đường tiệm cận xiên của đồ thị hàm số.

b) y = $\frac{3x^2+8x-2}{x+3}$

Ta có: $\underset{x\to -3^{+}}{\lim }y=\underset{x\to -3^{+}}{\lim }\frac{3x^2+8x-2}{x+3}=+\infty$ ;

          $\underset{x\to -3^{-}}{\lim }y=\underset{x\to -3^{-}}{\lim }\frac{3x^2+8x-2}{x+3}=-\infty$

Do đó đường thẳng x = −3 là tiệm cận đứng của đồ thị hàm số.

           $\underset{x\to +\infty }{\lim }\frac{y}{x}=\underset{x\to +\infty }{\lim }\frac{3x^2+8x-2}{\left(x+3\right)x}=3$ .

           $\underset{x\to +\infty }{\lim }\left(y-3x\right)=\underset{x\to +\infty }{\lim }\left[\frac{3x^2+8x-2}{x+3}-3x\right]=\underset{x\to +\infty }{\lim }\frac{-x-2}{x-2}=-1$.

Do đó đường thẳng y = 3x – 1 là tiệm cận xiên của đồ thị hàm số.

Bài 1.24 trang 19 SBT Toán 12 Tập 1: Cho hàm số y = f(x) có bảng biến thiên như sau:

Hãy tìm các tiệm cận đứng và tiệm cận ngang và đồ thị hàm số đã cho.

Lời giải:

Dựa vào bảng biến thiên, ta thấy:

$\underset{x\to 2^{+}}{\lim }y$ = −∞; $\underset{x\to 2^{-}}{\lim }y$  = +∞.

Do đó, đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.

$\underset{x\to +\infty }{\lim }y$ = 3, do đó đường thẳng y = 3 là tiệm cận ngang của đồ thị hàm số.

Bài 1.25 trang 19 SBT Toán 12 Tập 1: Cho hàm số y = f(x) có bảng biến thiên như sau:

Tìm các đường tiệm cận ngang của đồ thị hàm số $y=g\left(x\right)=\frac{1}{2+f\left(x\right)}.$

Lời giải:

Dựa vào bảng biến thiên, ta có: $\underset{x\to +\infty }{\lim }f\left(x\right)$  = 1 và $\underset{x\to -\infty }{\lim }f\left(x\right)$  = −1.

Suy ra $\underset{x\to +\infty }{\lim }g\left(x\right)$  = $\underset{x\to +\infty }{\lim }\frac{1}{2+f\left(x\right)}$  = $\frac{1}{3}$

          $\underset{x\to -\infty }{\lim }g\left(x\right)$  = $\underset{x\to -\infty }{\lim }\frac{1}{2+f\left(x\right)}$  = −1 

Do đó, đường thẳng y = −1 và y = $\frac{1}{3}$  là hai đường tiệm cận ngang của đồ thị hàm số g(x).  

Bài 1.26 trang 20 SBT Toán 12 Tập 1: Cho hàm số $y=\frac{x+1}{x-1}$  có đồ thị (C). Tính tích khoảng cách từ một điểm tùy ý thuộc (C) đến hai đường tiệm cận của nó.

Lời giải:

Ta có: $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{x+1}{x-1}=1$ ;

          $\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{x+1}{x-1}=1$ .

Do đó, đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.

          $\underset{x\to 1^{+}}{\lim }y=\underset{x\to 1^{+}}{\lim }\frac{x+1}{x-1}=+\infty$ ;

          $\underset{x\to 1^{-}}{\lim }y=\underset{x\to 1^{-}}{\lim }\frac{x+1}{x-1}=-\infty$ .

Do đó đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.

Vậy đồ thị hàm số đã cho có đường tiệm cận đứng là đường thẳng x = 1 và tiệm cận ngang y = 1.

Lấy M(x₀; y₀) ∈ (C) với $y_0=\frac{x_0+1}{x_0-1}$ .

Ta có: khoảng cách từ M đến đường tiệm cận đứng là d₁ = | x₀ – 1|, khoảng cách từ M đến tiệm cận ngang là d₂ = $\left|\frac{x_0+1}{x_0-1}-1\right|=\frac{2}{\left|x_0-1\right|}$ .

Vậy tích khoảng cách là:d₁d₂ = $\left|x_0–1\right|$ . $\frac{2}{\left|x_0-1\right|}$  = 2.

Bài 1.27 trang 20 SBT Toán 12 Tập 1: Gọi I là giao điểm giữa tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\frac{2x+3}{x-2}$ . Cho điểm K(3; 5), tính hệ số góc của đường thẳng qua I và K.

Lời giải:

Ta có: $\underset{x\to 2^{+}}{\lim }y=\underset{x\to 2^{+}}{\lim }\frac{2x+3}{x-2}=+\infty$ ;

           $\underset{x\to 2^{-}}{\lim }y=\underset{x\to 2^{-}}{\lim }\frac{2x+3}{x-2}=-\infty$ .

Do đó, đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.

          $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{2x+3}{x-2}=2$ ;

           $\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{2x+3}{x-2}=2$ .

Do đó, đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.

Suy ra điểm I(2; 2).

Đường thẳng đi qua I(2; 2) và K(3; 5) có hệ số góc là: a = $\frac{5-2}{3-2}=3$ .

Vậy hệ số góc của đường thẳng đi qua hai điểm I và K là 3.

Bài 1.28 trang 20 SBT Toán 12 Tập 1: Cho hàm số $y=f\left(x\right)=\frac{\sqrt{x^2+3}}{x-1}$  có đồ thị như hình sau:

Hãy tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho.

Lời giải:

Ta có: $\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }\frac{\sqrt{x^2+3}}{x-1}=+\infty$ ;

           $\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }\frac{\sqrt{x^2+3}}{x-1}=-\infty$ .

Do đó, đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.

          $\underset{x\to -\infty }{\lim }f\left(x\right)=\underset{x\to -\infty }{\lim }\frac{\sqrt{x^2+3}}{x-1}=-1$ ;

           $\underset{x\to +\infty }{\lim }f\left(x\right)=\underset{x\to +\infty }{\lim }\frac{\sqrt{x^2+3}}{x-1}=1$ .

Do đó, đường thẳng y = 1 và y = −1 là đường tiệm cận ngang của đồ thị hàm số.

Bài 1.29 trang 20 SBT Toán 12 Tập 1: Cho hàm số $y=f\left(x\right)=\frac{x+2}{x-3}$  có đồ thị (C). Gọi tổng khoảng cách từ một điểm (x; y) ∈ (C), với x > 3, tới hai đường tiệm cận của (C) là g(x). Tìm các đường tiệm cận của đồ thị hàm số y = g(x).

Lời giải:

Đồ thị hàm số f(x) có đường tiệm cận đứng là đường thẳng x = 3 và đường tiệm cận ngang là đường thẳng y = 1.

Khoảng cách từ điểm M(x; y) ∈ (C), x > 3 đến tiệm cận đứng là d₁ = x – 3.

Khoảng cách từ điểm M đến đường tiệm cận ngang là d₂ = $\frac{x+2}{x-3}-1=\frac{5}{x-3}$ .

Vậy g(x) = d₁ + d₂ = x – 3 + $\frac{5}{x-3}$ .

Ta có: $\underset{x\to -\infty }{\lim }g\left(x\right)=\underset{x\to -\infty }{\lim }\left[x–3+\frac{5}{x-3}\right]=-\infty .$ ;

          $\underset{x\to +\infty }{\lim }g\left(x\right)=\underset{x\to +\infty }{\lim }\left[x–3+\frac{5}{x-3}\right]=+\infty .$

Do đó đồ thị hàm số g(x) không có tiệm cận ngang

          $\underset{x\to 3^{-}}{\lim }g\left(x\right)=\underset{x\to 3^{-}}{\lim }\left[x–3+\frac{5}{x-3}\right]=-\infty .$ ;

          $\underset{x\to 3^{+}}{\lim }g\left(x\right)=\underset{x\to 3^{+}}{\lim }\left[x–3+\frac{5}{x-3}\right]=+\infty .$

Do đó, đường thẳng x = 3 là đường tiệm cận đứng của đồ thị hàm số

  $\underset{x\to +\infty }{\lim }\left(g\left(x\right)-(x-3)\right)=\underset{x\to +\infty }{\lim }\left[x–3+\frac{5}{x-3}-(x-3)\right]=\underset{x\to +\infty }{\lim }\frac{5}{x-3}=0.$

Do đó đường thẳng y = x – 3 là đường tiệm cận xiên của đồ thị hàm số.

Bài 1.30 trang 20 SBT Toán 12 Tập 1: Một bình chứa 200 ml dung dịch muối với nồng độ 5 mg/ml.

a) Tính nồng độ dung dịch muối trong bình sau khi thêm vào x ml dung dịch muối với nồng độ 10 mg/ml.

b) Phải thêm bao nhiêu mililít vào bình để có dung dịch muối với nồng độ 9 mg/ml? Nồng độ muối trong bình có thể đạt đến 10 mg/ml được không?

Lời giải:

a) Nồng độ dung dịch muối sau khi thêm vào x ml dung dịch muối với nồng độ 10 mg/ml là: C(x) = $\frac{200.5+10.x}{200+x}=\frac{1000+10x}{200+x}$ .

b) Để dung dịch muối với nồng độ 9mg/ml, ta phải thêm vào bình x ml với x thỏa mãn

C(x) = 9 ⇔ $\frac{1000+10x}{200+x}$ = 9 ⇔ x = 800 (ml).

Ta có: C(x) = $\frac{1000+10x}{200+x}$

           C'(x) = $\frac{1000}{x+200}$  > 0, ∀x ∈ (0; +∞).

Hàm C(x) luôn đồng biến trên khoảng (0; +∞).

Nhận thấy $\underset{x\to +\infty }{\lim }C\left(x\right)=\underset{x\to +\infty }{\lim }\frac{1000+10x}{200+x}=10$ .

Do đó, nồng độ muối trong bình không thể đạt đến 10 mg/ml.

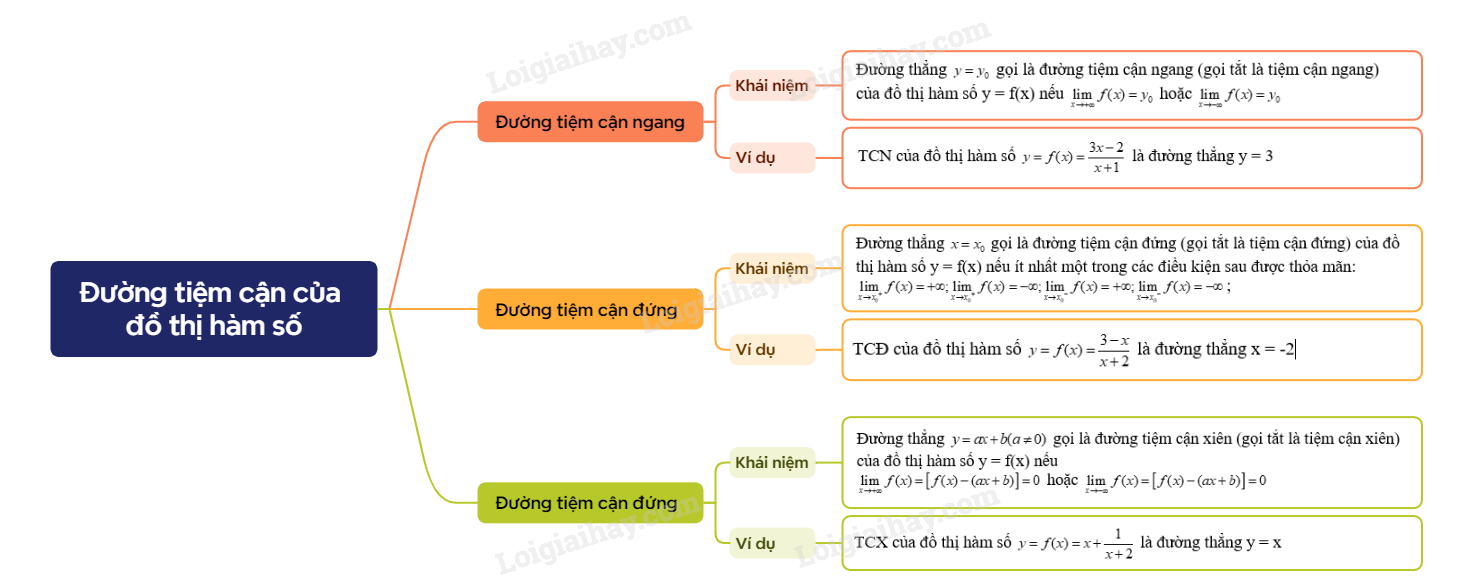
Lý thuyết Đường tiệm cận của đồ thị hàm số

1. Đường tiệm cận ngang

Đường thẳng $y=y_0$ gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số y = f(x) nếu $\underset{x\to +\mathrm{\infty }}{lim}f(x)=y_0$ hoặc $\underset{x\to -\mathrm{\infty }}{lim}f(x)=y_0$

Ví dụ: Tìm TCN của đồ thị hàm số $y=f(x)=\frac{3x-2}{x+1}$

Ta có: $\underset{x\to +\mathrm{\infty }}{lim}\frac{3x-2}{x+1}=\underset{x\to -\mathrm{\infty }}{lim}\frac{3x-2}{x+1}=3$

Vậy đồ thị hàm số f(x) có TCN là y = 3.

2. Đường tiệm cận đứng

Đường thẳng $x=x_0$ gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:$\underset{x\to {x_0}^{+}}{lim}f(x)=+\mathrm{\infty };\underset{x\to {x_0}^{+}}{lim}f(x)=-\mathrm{\infty };\underset{x\to {x_0}^{-}}{lim}f(x)=+\mathrm{\infty };\underset{x\to {x_0}^{-}}{lim}f(x)=-\mathrm{\infty }$;

Ví dụ: Tìm TCĐ của đồ thị hàm số $y=f(x)=\frac{3-x}{x+2}$

Ta có: $\underset{x\to -2^{+}}{lim}\frac{3x-2}{x+2}=+\mathrm{\infty }$

Vậy đồ thị hàm số có TCĐ là x = -2

3. Đường tiệm cận xiên

Đường thẳng $y=ax+b(a\ne 0)$ gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số y = f(x) nếu $\underset{x\to +\mathrm{\infty }}{lim}f(x)=\left[f(x)-(ax+b)\right]=0$ hoặc $\underset{x\to -\mathrm{\infty }}{lim}f(x)=\left[f(x)-(ax+b)\right]=0$

Ví dụ: Tìm TCX của đồ thị hàm số $y=f(x)=x+\frac{1}{x+2}$

Ta có: $\underset{x\to +\mathrm{\infty }}{lim}\left[f(x)-x\right]=\underset{x\to +\mathrm{\infty }}{lim}\frac{1}{x+2}=0$

Vậy đồ thị hàm số có TCX là y = x

Sơ đồ tư duy Đường tiệm cận của đồ thị hàm số

Xem thêm các bài giải SBT Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Bài 3: Đường tiệm cận của đồ thị hàm số

Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn

Bài tập cuối chương 1

Bài 6: Vectơ trong không gian