Đề luyện tập GHK2 Toán 12 – 2025 – Quốc Thái
Phần I. Trắc nghiệm 1 đáp án đúng
Trong không gian \(Oxyz\), cho đường thẳng \(\Delta\) có phương trình \(\dfrac{x-2}{1}=\dfrac{y+1}{-2}=\dfrac{z-3}{3}\). Điểm nào dưới đây thuộc đường thẳng \(\Delta\)?
Trong không gian \(Oxyz\), cho hai điểm \(A(1;-2;-3)\) và \(B(2;4;5)\). Phương trình chính tắc của đường thẳng \(AB\) là
Trong không gian \(Oxyz\), đường thẳng qua \(R(4;-2;0)\) và vuông góc với mặt phẳng \(\alpha\): \(2x+3y-z+6=0\)
có phương trình là
Trong không gian \(Oxyz\), phương trình mặt cầu tâm \(I(-2;1;3)\) bán kính \(R=7\) có phương trình là
Nguyên hàm của hàm số \(f(x)=6x-\dfrac{1}{x}\) (với \(x > 0)\) là
Trong không gian \(Oxyz\), cho mặt phẳng $(P):-2x+3y+z-5=0$. Vectơ pháp tuyến của (P) là
Trong không gian \(Oxyz\), phương trình mặt phẳng đi qua điểm \(F(-2;1;3)\) và có vectơ pháp tuyến \(\vec{n}=(1;-3;2)\) là
Trong không gian \(Oxyz\), đường thẳng \(\left\{\begin{array}{{20}{l}}x=1+2t\\y=1+t\\z=2+t\end{array}\right.\) cắt mặt phẳng \(Oxz\) tại điểm có tọa độ là
Biết \(F(x)=x^{3}-2x\) là một nguyên hàm của hàm số \(f(x)\). Giá trị của tích phân \(\int_0^1f(x)dx\) bằng
Trong không gian $Oxyz$, cho mặt cầu $\left(S\right):x^{2}+y^{2}+z^{2}-4x+6y-8z-7=0$. Bán kính của mặt cầu là
Cho hình phẳng \(H\) giới hạn bởi đồ thị hàm số \(y = f(x)\), trục hoành, trục tung và đường thẳng \(x = -4\) như hình bên. Diện tích của hình phẳng \(H\) đã cho là 
Một vật chuyển động chậm dần đều với vận tốc $v\left(t\right)=240-12t\left(\mathrm{\,\;m}/\mathrm{\,s}\right)$. Quãng đường mà vật chuyển động từ thời điểm $t=0\left(\mathrm{\,\;s}\right)$ đến thời điểm mà vật dừng lại là
Biết $F\left(x\right)$ là nguyên hàm của hàm số $y=f\left(x\right)$ trên đoạn $\begin{bmatrix}1;5\end{bmatrix}$ và thoả mãn $F\left(1\right)=5$ và $F\left(5\right)=2$, giá trị của biểu thức là
Cho hàm số \(y = f(x)\) liên tục trên \(\mathbb{R}\), thoả mãn \(\int_{2}^{4} f(x) dx = 8\) và \(\int_{4}^{6} f(x) dx = 12\). Biểu thức \(\int_{2}^{6} f(x) dx\) bằng
Trong không gian $Oxyz$, đường thẳng $d:\dfrac{x+3}{1}=\dfrac{y-1}{-1}=\dfrac{z-5}{2}$ có một vectơ chỉ phương là
Trong không gian $Oxyz$, mặt phẳng $Oxz$ có phương trình là
Nguyên hàm của hàm số $f\left(x\right)=\dfrac{1}{x^{2}}$ (với $x\neq 0$ ) là
Cho hình phẳng \(H\) giới hạn bởi đồ thị hàm số \(y = f(x)\), trục hoành và hai đường thẳng \(x = a\), \(x = b\) như hình bên. Khi quay \(H\) quanh trục hoành, thể tích khối tròn xoay thu được bằng 
Trong không gian $Oxyz$, cho mặt phẳng $\left(Q\right):x+2y-2z+1=0$ và điểm $M\left(1;-2;1\right)$. Khoảng cách từ điểm $M$ đến mặt phẳng $\left(Q\right)$ bằng
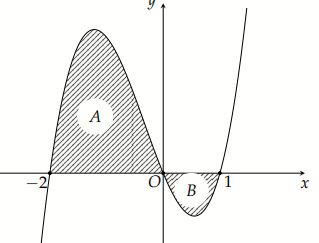
Cho hàm số hàm số $y=f\left(x\right)$ có đồ thị là đường cong trong hình bên. Biết $\int_{-2}^{0}f(x)dx=\frac{14}{3}$. Khi đó, diện tích phần gạch sọc bằng 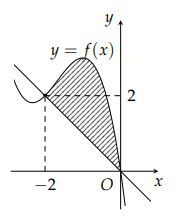
Phần II. Đúng sai
Trong không gian với hệ tọa độ $Oxyz$, cho 2 điểm $A\left(1;2;-1\right),B\left(-1;0;1\right)$ và mặt phẳng $(P):x+2y-z+1=0$.
Trong không gian $Oxyz$, cho mặt cầu $\left(S\right):x^{2}+y^{2}+z^{2}-2x+4y+8z+5=0$; điểm $A\left(2;-3;1\right)$ và $B\left(5;-7;0\right)$.
Cho hai hàm số $f\left(x\right)=x^{2}$ và $g\left(x\right)=\dfrac{1}{3}x^{3}-2x$ có đồ thị lần lượt là $\left(C_{1}\right),\left(C_{2}\right)$
Một chất điểm đang chuyển động với vận tốc $v_{\circ }=16\left(\mathrm{\,\;m}/\mathrm{\,s}\right)$ thì tăng tốc với gia tốc $a\left(t\right)=$ $t^{2}+3t\left(\mathrm{\,\;m}/\mathrm{\,s}^{2}\right)$.
Phần III. Trả lời ngắn