Câu hỏi:
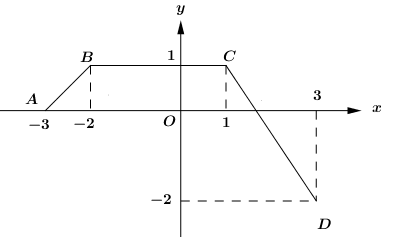
Cho hàm số f(x) có đồ thị trên đoạn \(\left[ { – 3;3} \right]\;\)là đường gấp khúc ABCD như hình vẽ.
Tính \(\mathop \smallint \limits_{ – 3}^3 f\left( x \right)dx\)
A.\(\frac{5}{2}\)
Đáp án chính xác
B. \(\frac{{35}}{6}\)
C. \(\frac{{ – 5}}{2}\)
D. \(\frac{{ – 35}}{6}\)
Trả lời:
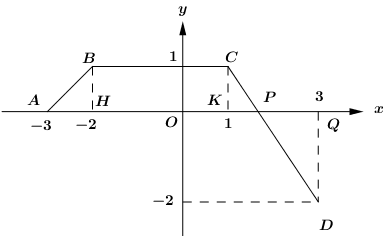
Ta có:
\(\begin{array}{*{20}{l}}{\mathop \smallint \limits_{ – 3}^3 f\left( x \right)dx = {S_{ABH}} + {S_{BCKH}} + {S_{CPK}} – {S_{DPQ}}}\\{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}.1.1 + 3.1 + \frac{1}{2}.1.\frac{2}{3} – \frac{1}{2}.\frac{4}{3}.2 = \frac{5}{2}}\end{array}\)
Đáp án cần chọn là: A
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), đường thẳng y=0 và hai đường thẳng \(x = a,x = b(a < b)\) là: – ĐGNL-HN
Câu hỏi:
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), đường thẳng y=0 và hai đường thẳng \(x = a,x = b(a < b)\) là:
A. \(S = \mathop \smallint \limits_a^b f\left( x \right)dx\)
B. \(S = \mathop \smallint \limits_0^b f\left( x \right)dx\)
C. \(S = \mathop \smallint \limits_b^a \left| {f\left( x \right)} \right|dx\)
D. \(S = \mathop \smallint \limits_a^b \left| {f\left( x \right)} \right|dx\)
Đáp án chính xác
Trả lời:
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số\(y = f\left( x \right)\) đường thẳng y=0 và hai đường thẳng\(x = a,x = b\) là\(S = \mathop \smallint \limits_a^b \left| {f\left( x \right)} \right|dx\)
Đáp án cần chọn là: D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = {x^2} – 1\), trục hoành và hai đường thẳng x=−1;x=−3 là: – ĐGNL-HN
Câu hỏi:
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = {x^2} – 1\), trục hoành và hai đường thẳng x=−1;x=−3 là:
A.\(S = \mathop \smallint \limits_{ – 3}^{ – 1} \left| {{x^2} – 1} \right|dx\)
Đáp án chính xác
B. \(S = \mathop \smallint \limits_{ – 1}^{ – 3} \left| {{x^2} – 1} \right|dx\)
C. \(S = \mathop \smallint \limits_{ – 3}^0 \left| {{x^2} – 1} \right|dx\)
D. \(S = \mathop \smallint \limits_{ – 3}^{ – 1} \left( {1 – {x^2}} \right)dx\)
Trả lời:
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số\(y = f\left( x \right) = {x^2} – 1\) trục hoành và hai đường thẳng \(x = – 1;x = – 3\) là:\(S = \mathop \smallint \limits_{ – 3}^{ – 1} \left| {{x^2} – 1} \right|dx\)
Đáp án cần chọn là: A====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng \(x = a,x = b(a < b)\;\) là: – ĐGNL-HN
Câu hỏi:
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng \(x = a,x = b(a < b)\;\) là:
A.\(S = \mathop \smallint \limits_a^b \left( {f\left( x \right) – g\left( x \right)} \right)dx\)
B. \(S = \mathop \smallint \limits_a^b \left( {g\left( x \right) – f\left( x \right)} \right)dx\)
C. \(S = \mathop \smallint \limits_a^b \left| {f\left( x \right) – g\left( x \right)} \right|dx\)
Đáp án chính xác
D. \(S = \mathop \smallint \limits_a^b \left| {f\left( x \right)} \right|dx – \mathop \smallint \limits_a^b \left| {g\left( x \right)} \right|dx\)
Trả lời:
Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số\(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng\(x = a,x = b(a < b)\) là:\(S = \mathop \smallint \limits_a^b \left| {f\left( x \right) – g\left( x \right)} \right|dx\)
Đáp án cần chọn là: C====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hai hàm số \(f(x) = – x\;\) và \(g(x) = {e^x}\). Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y = f(x),y = g(x)\;\) và hai đường thẳng x=0,x=e là: – ĐGNL-HN
Câu hỏi:
Cho hai hàm số \(f(x) = – x\;\) và \(g(x) = {e^x}\). Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y = f(x),y = g(x)\;\) và hai đường thẳng x=0,x=e là:
A.\(S = \mathop \smallint \limits_0^e \left| {{e^x} + x} \right|dx\)
Đáp án chính xác
B. \(S = \mathop \smallint \limits_0^e \left| {{e^x} – x} \right|dx\)
C. \(S = \mathop \smallint \limits_e^0 \left| {{e^x} – x} \right|dx\)
D. \(S = \mathop \smallint \limits_e^0 \left| {{e^x} + x} \right|dx\)
Trả lời:
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số\(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng \(x = 0,x = e\) là:
\(S = \mathop \smallint \limits_0^e \left| {{e^x} – \left( { – x} \right)} \right|dx = \mathop \smallint \limits_0^e \left| {{e^x} + x} \right|dx\)Đáp án cần chọn là: A
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y = {x^3} – x;y = 2x\) và các đường thẳng \(x = – 1;x = 1\;\) được xác định bởi công thức: – ĐGNL-HN
Câu hỏi:
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y = {x^3} – x;y = 2x\) và các đường thẳng \(x = – 1;x = 1\;\) được xác định bởi công thức:
A.\(S = \left| {\mathop \smallint \nolimits_{ – 1}^1 \left( {3x – {x^3}} \right)dx} \right|\)
B. \(S = \mathop \smallint \nolimits_{ – 1}^0 \left( {3x – {x^3}} \right)dx + \mathop \smallint \nolimits_0^1 \left( {{x^3} – 3x} \right)dx\)
C. \(S = \mathop \smallint \nolimits_{ – 1}^1 \left( {3x – {x^3}} \right)dx\)
D. \(S = \mathop \smallint \nolimits_{ – 1}^0 \left( {{x^3} – 3x} \right)dx + \mathop \smallint \nolimits_0^1 \left( {3x – {x^3}} \right)dx\)
Đáp án chính xác
Trả lời:
Xét phương trình hoành độ giao điểm của 2 đồ thị:
\({x^3} – x = 2x \Leftrightarrow {x^3} – 3x = 0 \Leftrightarrow x = 0\) (chỉ xét trên\(\left( { – 1;1} \right)\)
Với\(x \in \left( { – 1;0} \right)\) thì\({x^3} – 3x > 0\) với \(x \in \left( {0;1} \right)\) thì \({x^3} – 3x < 0\)
Diện tích cần tìm là \(S = \mathop \smallint \limits_{ – 1}^1 \left| {{x^3} – 3x} \right|dx = \mathop \smallint \limits_{ – 1}^0 \left( {{x^3} – 3x} \right)dx + \mathop \smallint \limits_0^1 \left( {3x – {x^3}} \right)dx\)Đáp án cần chọn là: D
====== **** mời các bạn xem câu tiếp bên dưới **** =====
