Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M,N lần lượt là trung điểm của các cạnh AB,BC. Điểm I thuộc đoạn SA. Biết mặt phẳng (MNI) chia khối chóp S.ABCD  thành hai phần, phần chứa đỉnh S có thể tích bằng 725 lần phần còn lại. Tính tỉ số IAIS?

Câu hỏi:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M,N lần lượt là trung điểm của các cạnh AB,BC. Điểm I thuộc đoạn SA. Biết mặt phẳng (MNI) chia khối chóp S.ABCD  thành hai phần, phần chứa đỉnh S có thể tích bằng $\frac{7}{25}$ lần phần còn lại. Tính tỉ số $\frac{IA}{IS}$?

A. $\frac{5}{3}$

Đáp án chính xác

B. $\frac{2}{3}$

C. $\frac{3}{2}$

D. $\frac{3}{5}$

Trả lời:

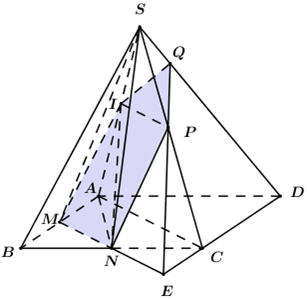
Giả sử $SC\cap \left(IMN\right)=\left\{P\right\}\Rightarrow \left(IMN\right)\cap \left(SAC\right)=IP$
Ta có: $\left\{\begin{array}{c}\left(IMN\right)\cap \left(SAC\right)=IP\\ \left(IMN\right)\cap \left(ABCD\right)=MN\\ \left(SAC\right)\cap \left(ABCD\right)=AC\end{array}\right.\Rightarrow IP\parallel MN\parallel AC$
Trong (ABCD) gọi $\left\{E\right\}=MN\cap CD$ trong (SCD) gọi $Q=NP\cap SD$
Khi đó thiết diện của hình chóp cắt bởi (MNI) là ngũ giác IMNPQ.
Gọi $V_1=V_{S.BMNPQI},V=V_{S.ABCD}$theo bài ra ta có $V_1=\frac{7}{32}V$
Ta có $V_1=V_{S.BMN}+V_{S.IMN}+V_{S.INP}+V_{S.IPQ}$
Đặt $\frac{SI}{SA}=x(0<x<1)$ áp dụng định lí Ta-lét ta có $\frac{SI}{SA}=\frac{SP}{SC}=x$
– Xét khối chóp S.BMN và S.ABCD:
  + Có cùng chiều cao (cùng bằng khoảng cách từ SS đến (ABCD)).
$S_{BMN}=\frac{1}{4}{S}_{ABC}=\frac{1}{8}{S}_{ABC}$(do tam giác BMN và tam giác BAC đồng dạng theo tỉ số $\frac{1}{2}$)
Do đó $V_{S.BMN}=\frac{1}{8}{V}_{S.ABCD}=\frac{1}{8}V$
– Xét khối chóp S.IMN và S.AMN:
$\frac{V_{S.INP}}{V_{S.ANC}}=\frac{SI}{SA}.\frac{SP}{SC}=x^2\Rightarrow V_{S.IMN}=x^2.V_{S.ANC}$
Ta có $S_{ANC}=\frac{1}{2}{S}_{ABC}=\frac{1}{4}{S}_{ABCD}\Rightarrow V_{S.ANC}=\frac{1}{4}V\Rightarrow V_{S.IMN}=\frac{x^2}{4}V$
– Xét khối chóp S.IPQ và S.ACD: $\frac{V_{S.IPQ}}{V_{S.ACD}}=\frac{SI}{SA}.\frac{SP}{SC}.\frac{SQ}{SD}$
Ta có AMEC là hình bình hành nên $EC=AM=\frac{1}{2}CD\Rightarrow \frac{EC}{ED}=\frac{1}{3}$
Áp dụng định lí Menelaus trong tam giác SCD với cát tuyến EPQ ta có:
$\frac{PS}{PC}.\frac{EC}{ED}.\frac{QD}{QS}=1\Rightarrow \frac{x}{1-x}.\frac{1}{3}.\frac{QD}{QS}=1$
$\begin{array}{l}\Rightarrow \frac{QD}{QS}=\frac{3\left(1-x\right)}{x}\Rightarrow \frac{SQ}{QD}=\frac{x}{3\left(1-x\right)}\\ \Rightarrow \frac{SQ}{SQ+QD}=\frac{x}{x+3\left(1-x\right)}\\ \Rightarrow \frac{SQ}{SD}=\frac{x}{3-2x}\end{array}$
Suy ra $\frac{V_{S.IPQ}}{V_{S.ACD}}=\frac{SI}{SA}.\frac{SP}{SC}.\frac{SQ}{SD}=x^2.\frac{x}{3-2x}=\frac{x^3}{3-2x}$
$\Rightarrow V_{S.IPQ}=\frac{x^3}{3-2x}{V}_{S.ACD}$
Mà $S_{ACD}=\frac{1}{2}{S}_{ABCD}\Rightarrow V_{S.ACD}=\frac{1}{2}V\Rightarrow V_{S.IPQ}=\frac{x^3}{2\left(3-2x\right)}V$
Khi đó ta có:
$V_1=V_{S.BMN}+V_{S.IMN}+V_{S.INP}+V_{S.IPQ}$
$\Rightarrow V_1=\frac{1}{8}V+\frac{x}{8}V+\frac{x^2}{4}V+\frac{x^3}{2(3-2x)}V$
$\Rightarrow V_1=\left(\frac{1}{8}+\frac{x}{8}+\frac{x^2}{4}+\frac{x^3}{2(3-2x)}\right)V=\frac{7}{32}v$
$\Rightarrow \frac{1}{8}+\frac{x}{8}+\frac{x^2}{4}+\frac{x^3}{2(3-2x)}=\frac{7}{32}$
$\iff \frac{1+x+2x^2}{4}+\frac{x^3}{3-2x}=\frac{7}{16}$
$\iff (1+x+2x^2).(12-8x)+16x^3=7(3-2x)$
$\iff 12+12x+24x^2-8x-8x^2-16x^3+16x^3=21-14x$
$\iff 16x^2+18x-9=0\iff \left[\begin{array}{c}x=\frac{3}{8}\left(tm\right)\\ x=-\frac{3}{2}\left(ktm\right)\end{array}\right.$
$\Rightarrow \frac{SI}{SA}=\frac{3}{8}\Rightarrow \frac{IS}{IA}=\frac{3}{5}\Rightarrow \frac{IA}{IS}=\frac{5}{3}$
Đáp án cần chọn là: A

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho khối chóp có thể tích V, diện tích đáy là S và chiều cao h. Chọn công thức đúng:
   
   

   Câu hỏi:
   

   Cho khối chóp có thể tích V, diện tích đáy là S và chiều cao h. Chọn công thức đúng:

   A. $V=Sh$

   B. $V=\frac{1}{2}Sh$

   C. $V=\frac{1}{3}Sh$

   Đáp án chính xác

   D. $V=\frac{1}{6}Sh$

   Trả lời:

   Công thức tính thể tích khối chóp $V=\frac{1}{3}Sh$

   Đáp án cần chọn là: C

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Phép vị tự tỉ số k &gt; 0 biến khối chóp có thể tích V thành khối chóp có thể tích V′. Khi đó:
   
   

   Câu hỏi:
   

   Phép vị tự tỉ số k > 0 biến khối chóp có thể tích V thành khối chóp có thể tích V′. Khi đó:

   A. $\frac{V}{V^{‘}}=k$

   B. $\frac{V^{‘}}{V}=k^2$

   C. $\frac{V}{V^{‘}}=k^3$

   D. $\frac{V^{‘}}{V}=k^3$

   Đáp án chính xác

   Trả lời:

   Phép vị tự tỉ số k > 0 biến khối chóp có thể tích V thành khối chóp có thể tích V′. Khi đó $\frac{V^{‘}}{V}=k^3$
   Đáp án cần chọn là: D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho khối chóp tam giác S.ABC, trên các cạnh SA,SB,SC lần lượt lấy các điểm A′,B′,C′. Khi đó:
   
   

   Câu hỏi:
   

   Cho khối chóp tam giác S.ABC, trên các cạnh SA,SB,SC lần lượt lấy các điểm A′,B′,C′. Khi đó:

   A. $\frac{V_{S.A^{‘}{B}^{‘}{C}^{‘}}}{V_{S.ABC}}=\frac{S{A}^{‘}}{SA}+\frac{S{B}^{‘}}{SB}+\frac{S{C}^{‘}}{SC}$

   B. $\frac{V_{S.ABC}}{V_{S.A^{‘}{B}^{‘}{C}^{‘}}}=\frac{S{A}^{‘}}{SA}.\frac{S{B}^{‘}}{SB}.\frac{S{C}^{‘}}{SC}$

   C. $\frac{V_{S.A^{‘}{B}^{‘}{C}^{‘}}}{V_{S.ABC}}=\frac{S{A}^{‘}}{SA}=\frac{S{B}^{‘}}{SB}=\frac{S{C}^{‘}}{SC}$

   D. $\frac{V_{S.A^{‘}{B}^{‘}{C}^{‘}}}{V_{S.ABC}}=\frac{S{A}^{‘}}{SA}.\frac{S{B}^{‘}}{SB}.\frac{S{C}^{‘}}{SC}$

   Đáp án chính xác

   Trả lời:

   Nếu $A^{‘},B^{‘},C^{‘}$ là ba điểm lần lượt nằm trên các cạnh $SA,SB,SC$ của hình chóp tam giác S.ABC. Khi đó:
   $\frac{V_{S.A^{‘}{B}^{‘}{C}^{‘}}}{V_{S.ABC}}=\frac{S{A}^{‘}}{SA}.\frac{S{B}^{‘}}{SB}.\frac{S{C}^{‘}}{SC}$
   Đáp án cần chọn là: D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Đáy của hình chóp S.ABCD là một hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy và có độ dài là a. Thể tích khối tứ diện S.BCD bằng:
   
   

   Câu hỏi:
   

   Đáy của hình chóp S.ABCD là một hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy và có độ dài là a. Thể tích khối tứ diện S.BCD bằng:

   A. $\frac{a^3}{6}$

   Đáp án chính xác

   B. $\frac{a^3}{3}$

   B. $\frac{a^3}{4}$

   C. $\frac{a^3}{8}$

   Trả lời:

   Ta có: $S_{\text{Δ}BCD}=\frac{1}{2}{S}_{ABCD}=\frac{1}{2}{a}^2$m ;
   $V_{S.BCD}=\frac{1}{3}SA.S_{BCD}=\frac{1}{3}a.\frac{1}{2}{a}^2=\frac{a^3}{6}$
   

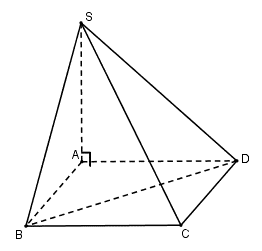
   Đáp án cần chọn là: A

    

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D thỏa mãn SA⊥ABCD  và AB=2AD=2CD=2a=2SA. Thể tích khối chóp S.BCD là:
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD có ABCD là hình thang vuông tại A và D thỏa mãn $SA\perp \left(ABCD\right)$ và $AB=2AD=2CD=2a=\sqrt{2}SA$. Thể tích khối chóp S.BCD là:

   A. $\frac{2a^3\sqrt{2}}{3}$

   B. $\frac{a^3\sqrt{2}}{6}$

   Đáp án chính xác

   C. $\frac{2a^3}{3}$

   D. $\frac{a^3\sqrt{2}}{12}$

   Trả lời:

   

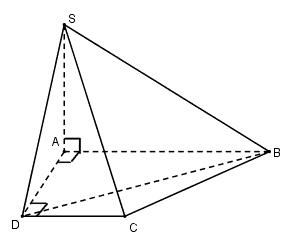
   Ta có: $S_{ABCD}=\frac{1}{2}\left(AB+CD\right).AD=\frac{1}{2}\left(2a+a\right)a=\frac{3a^2}{2}$
   $S_{\text{Δ}ABD}=\frac{1}{2}AD.AB=\frac{1}{2}a.2a=a^2$
   $\Rightarrow S_{BCD}=S_{ABCD}-S_{ABD}=\frac{3a^2}{2}-a^2=\frac{a^2}{2}SA=\frac{2a}{\sqrt{2}}=a\sqrt{2}$
   $\Rightarrow V_{S.BCD}=\frac{1}{3}SA.S_{BCD}=\frac{1}{3}a\sqrt{2}.\frac{a^2}{2}=\frac{a^3\sqrt{2}}{6}$
   Đáp án cần chọn là: B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====