Câu hỏi:
Để phương trình sau có 4 nghiệm phân biệt: \(\left| {10x – 2{x^2} – 8} \right| = {x^2} – 5x + a\) thì giá trị của tham số a là:
A.a=1.
B.\(a \in \left( {1;10} \right)\)
C. \(a \in \left[ {4;\frac{{45}}{4}} \right]\)
D. \(a \in \left( {4;\frac{{43}}{4}} \right)\)
Đáp án chính xác
Trả lời:
Xét phương trình: \(\left| {10x – 2{x^2} – 8} \right| = {x^2} – 5x + a\)(1)
\( \Leftrightarrow a = \left| {10x – 2{x^2} – 8} \right| – {x^2} + 5x\)
Xét \(f\left( x \right) = \left| {10x – 2{x^2} – 8} \right| – {x^2} + 5x\)
\( = \left\{ {\begin{array}{*{20}{c}}{(10x – 2{x^2} – 8) – {x^2} + 5x\,\,\,khi\,\,10x – 2{x^2} – 8 \ge 0}\\{ – (10x – 2{x^2} – 8) – {x^2} + 5x\,\,\,\,khi\,\,\,10x – 2{x^2} – 8 < 0}\end{array}} \right.\,\,\,\,\)
\( = \left\{ {\begin{array}{*{20}{c}}{ – 3{x^2} + 15x – 8\,\,\,khi\,\,\,1 \le x \le 4}\\{{x^2} – 5x + 8\,\,\,\,khi\,\,x \le 1 \vee x \ge 4}\end{array}} \right.\)
Bảng biến thiên:
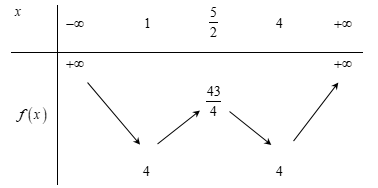
Dựa vào bảng biến thiên ta có phương trình (1) có 4 nghiệm phân biệt\( \Leftrightarrow 4 < a < \frac{{43}}{4}\)
Đáp án cần chọn là: D
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập nghiệm SS của bất phương trình \(5x – 1 \ge \frac{{2x}}{5} + 3\)là: – ĐGNL-HN
Câu hỏi:
Tập nghiệm SS của bất phương trình \(5x – 1 \ge \frac{{2x}}{5} + 3\)là:
A.\(S = \mathbb{R}.\)
B. \(S = \left( { – \infty ;2} \right).\)
C. \(S = \left( { – \frac{5}{2}; + \infty } \right).\)
D. \(S = \left[ {\frac{{20}}{{23}}; + \infty } \right).\)
Đáp án chính xác
Trả lời:
Bất phương trình\(5x – 1 \ge \frac{{2x}}{5} + 3\)
\( \Leftrightarrow 25x – 5 \ge 2x + 15 \Leftrightarrow 23x \ge 20 \Leftrightarrow x \ge \frac{{20}}{{23}}.\)
Đáp án cần chọn là: D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tổng các nghiệm nguyên của bất phương trình \(\frac{{x – 2}}{{\sqrt {x – 4} }} \le \frac{4}{{\sqrt {x – 4} }}\) bằng: – ĐGNL-HN
Câu hỏi:
Tổng các nghiệm nguyên của bất phương trình \(\frac{{x – 2}}{{\sqrt {x – 4} }} \le \frac{4}{{\sqrt {x – 4} }}\) bằng:
A.15.
B.11.
Đáp án chính xác
C.26.
D.0.
Trả lời:
Điều kiện: x >4.
Bất phương trình tương đương :
\(x – 2 \le 4 \Leftrightarrow x \le 6 \Rightarrow 4 < x \le 6\)
Mà \(x \in \mathbb{Z} \Rightarrow x = 5;x = 6 \Rightarrow S = 5 + 6 = 11\)
Đáp án cần chọn là: B
</>====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tổng các nghiệm nguyên của bất phương trình \(x\left( {2 – x} \right) \ge x\left( {7 – x} \right) – 6\left( {x – 1} \right)\) trên đoạn \(\left[ { – 10;10} \right]\;\)bằng: – ĐGNL-HN
Câu hỏi:
Tổng các nghiệm nguyên của bất phương trình \(x\left( {2 – x} \right) \ge x\left( {7 – x} \right) – 6\left( {x – 1} \right)\) trên đoạn \(\left[ { – 10;10} \right]\;\)bằng:
A.5.
B.6.
C.21.
D.40.
Đáp án chính xác
Trả lời:
Bất phương trình \(x\left( {2 – x} \right) \ge x\left( {7 – x} \right) – 6\left( {x – 1} \right)\)
\( \Leftrightarrow 2x – {x^2} \ge 7x – {x^2} – 6x + 6 \Leftrightarrow x \ge 6\)Mà\(x \in \mathbb{Z};x \in \left[ { – 10;10} \right] \Rightarrow x \in \left\{ {6;7;8;9;10} \right\}\)
Vậy tổng các nghiệm nguyên cần tìm là: 6+7+8+9+10=40.
Đáp án cần chọn là: D====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập nghiệm của bất phương trình: \( – {x^2} + 6x + 7\; \ge 0\;\) là: – ĐGNL-HN
Câu hỏi:
Tập nghiệm của bất phương trình: \( – {x^2} + 6x + 7\; \ge 0\;\) là:
A.\(\left( { – \infty ; – 1} \right] \cup \left[ {7; + \infty } \right)\)
B. \(\left[ { – 1;7} \right]\)
Đáp án chính xác
C. \(\left( { – \infty ; – 7} \right] \cup \left[ {1; + \infty } \right)\)
D. \(\left[ { – 7;1} \right]\)Trả lời:
Trả lời:
Ta có \( – {x^2} + 6x + 7 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 7}\\{x = – 1}\end{array}} \right.\)
Bảng xét dấu
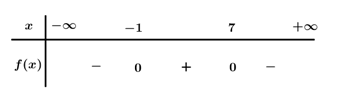
Dựa vào bảng xét dấu \( – {x^2} + 6x + 7\; \ge 0 \Leftrightarrow – 1 \le x \le 7.\)Đáp án cần chọn là: B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Giải bất phương trình \( – 2{x^2} + 3x – 7 \ge 0.\). – ĐGNL-HN
Câu hỏi:
Giải bất phương trình \( – 2{x^2} + 3x – 7 \ge 0.\).
A.S=0.
B.\(S = \left\{ 0 \right\}.\)
C. \(S = \emptyset .\)
Đáp án chính xác
D. \(S = \mathbb{R}.\)
Trả lời:
Ta có\( – 2{x^2} + 3x – 7\; = 0\) vô nghiệm.
Bảng xét dấu
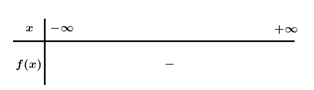
Dựa vào bảng xét dấu\( – 2{x^2} + 3x – 7 \ge 0\, \Leftrightarrow \,x \in \emptyset \)Đáp án cần chọn là: C
====== **** mời các bạn xem câu tiếp bên dưới **** =====
