Cho hàm số y=ax2+bx+c(a<0) có đồ thị (P). Khẳng định nào sau đây là khẳng định đúng? – ĐGNL-HN

Câu hỏi:

Cho hàm số $y=a{x}^2+bx+c(a<0)$ có đồ thị (P). Khẳng định nào sau đây là khẳng định đúng?

A.Hàm số đồng biến trên khoảng $\left(-\frac{b}{2a};+\infty \right)$

B.Hàm số nghịch biến trên khoảng $\left(-\infty ;-\frac{b}{2a}\right)$

C.Đồ thị luôn cắt trục hoành tại 2 điểm phân biệt.  

D.Đồ thị có trục đối xứng là đường thẳng $x=-\frac{b}{2a}$

Đáp án chính xác

Trả lời:

Hàm số $y=a{x}^2+bx+c(a<0)$đồng biến trên khoảng $\left(-\infty ;-\frac{b}{2a}\right)$ và nghịch biến trên khoảng $\left(-\frac{b}{2a};+\infty \right)$Nên A, B sai.
Ta chưa kết luận được gì về số giao điểm của đồ thị hàm số đã cho với trục hoành nên C sai.
Đồ thị hàm số $y=a{x}^2+bx+c\left(a\ne 0\right)$có trục đối xứng là đường thẳng $x=-\frac{b}{2a}$nên D đúng.
Đáp án cần chọn là: D

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Đường thẳng nào trong các đường thẳng sau đây là trục đối xứng của parabol y=−2×2+5x+3. – ĐGNL-HN
   
   

   Câu hỏi:
   

   Đường thẳng nào trong các đường thẳng sau đây là trục đối xứng của parabol $y=-2x^2+5x+3.$

   A.$x=\frac{5}{2}$

   B. $x=-\frac{5}{2}$

   C. $x=\frac{5}{4}$

   Đáp án chính xác

   D. $x=-\frac{5}{4}$

   Trả lời:

   Ta có:
   $\frac{-b}{2a}=\frac{-5}{2.(-2)}=\frac{5}{4}$
   Trục đối xứng là đường thẳng: $x=\frac{5}{4}.$Đáp án cần chọn là: C

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Đỉnh I của parabol (P): y=-3×2+6x−1 là: – ĐGNL-HN
   
   

   Câu hỏi:
   

   Đỉnh I của parabol (P): $y=–3x^2+6x-1$ là:

   A.I(1;2)

   Đáp án chính xác

   B.I(3;0) 

   C.I(2;−1)

   D.I(0;−1)

   Trả lời:

   Ta có:
   $\begin{array}{l}\frac{-b}{2a}=\frac{-6}{2.(-3)}=\frac{-6}{-6}=1\\ \frac{-\text{Δ}}{4a}=\frac{-(b^2-4ac)}{4a}=\frac{-6^2+4.(-3).(-1)}{4.(-3)}=\frac{-36+12}{-12}=\frac{-24}{-12}=2.\end{array}$
   Suy ra đỉnh của Parabol là: I(1;2)
   Đáp án cần chọn là: A

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Biết parabol (P):y=ax2+2x+5 đi qua điểm A(2;1). Giá trị của aa là: – ĐGNL-HN
   
   

   Câu hỏi:
   

   Biết parabol (P):$y={\text{ax}}^2+2x+5$ đi qua điểm A(2;1). Giá trị của aa là:

   A.a = -5

   B.a = -2

   Đáp án chính xác

   C. a = 2

   D. Một đáp số khác

   Trả lời:

   Parabol đi qua điểm A(2;1) nên ta có:4a + 4 + 5 = 1 ⇔ 4a = −8 ⇔ a = −2
   Đáp án cần chọn là: B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Đỉnh của parabol y=x2+x+mnằm trên đường thẳng y=34nếu m bằng: – ĐGNL-HN
   
   

   Câu hỏi:
   

   Đỉnh của parabol $y=x^2+x+m$nằm trên đường thẳng $y=\frac{3}{4}$nếu m bằng:

   A.Một số tùy ý

   B.3

   C.5

   D.1

   Đáp án chính xác

   Trả lời:

   Yêu cầu bài toán
   $\iff \frac{-b^2+4ac}{4a}=\frac{3}{4}\iff \frac{-1+4m}{4}=\frac{3}{4}\iff 4m=4\iff m=1$
   Đáp án cần chọn là: D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Bảng biến thiên của hàm số y=–x2+2x–1là: – ĐGNL-HN
   
   

   Câu hỏi:
   

   Bảng biến thiên của hàm số $y=–x^2+2x–1$là:

   A.

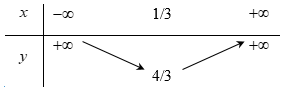
   B.

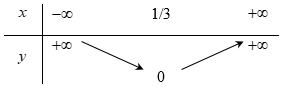
   C.

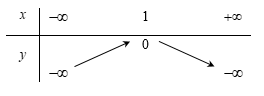
   Đáp án chính xác

   D.

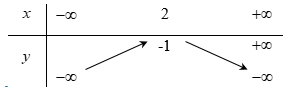
   Trả lời:

   Ta có:
   $a=-1<0;\frac{-b}{2a}=\frac{-2}{2.(-1)}=\frac{-2}{-2}=1$
   $y\left(1\right)=-1^2+2.1-1=0$
   Suy ra bảng biến thiên:
   
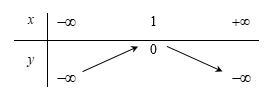
   Đáp án cần chọn là: C

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====